「2次方程式には解の公式がある。3次、4次にもある。しかし、5次以上には一般の代数的な解の公式は存在しない」
数学の歴史において、この事実は大きな衝撃をもって迎えられました。しかし、その一方で「具体的な解き方は分からなくても、複素数の範囲であれば n 次方程式には必ず n 個の解が存在する」という事実もまた、揺るぎない真理として確立されています。これが「代数学の基本定理」です。
既存の数学解説の多くは、リウヴィルの定理や最大値の原理を用いた形式的な証明に終止し、読者が抱く「なぜ実数ではダメで、複素数なら解けるのか?」という直感的な疑問や、証明の各ステップにおける論理の細部が置き去りにされがちです。
本稿では、幾何学的なイメージから論理の厳密な急所までを紐解き、この定理が数学の世界にどのような「完結」をもたらしたのかを解説します。
【幾何学的直感】複素平面を「覆う」軌跡のダイナミズム

代数学の基本定理の本質を理解するための第一歩は、数式を「複素平面上での点の動き」として捉え直すことです。
実数の範囲では、y = x^2 + 1 のようなグラフは x 軸(y=0)と交わらない場合があります。しかし、複素数 z を変数とする関数 f(z) を考えると、そこには「面」としての連続的な広がりが生まれます。
「犬の散歩」で考えるn次方程式の挙動
複素多項式 f(z) = a_n z^n + a_{n-1} z^{n-1} + \dots + a_0 が 0 になる理由を、「犬の散歩(ルーシェの定理の直感的解釈)」で考えてみましょう。
- 飼い主の支配力:複素平面上で、原点からの距離(半径)R を非常に大きく取ると、z^n の値は他のどの項よりも支配的になります。飼い主が原点の周りを R という巨大な半径で n 回まわるとき、犬はリードに繋がれているため、飼い主の勢いに抗って原点の反対側へ飛び出すことはできません。
- 原点を囲む軌跡:結果として、多項式 f(z) 全体が描く軌跡も、必ず原点を n 回囲むことになります。
連続的な収縮と原点の「通過」
次に、この巨大な円の半径 R を少しずつ小さくしていき、最終的に R = 0 にすることを想像してください。
- 半径 R が巨大なとき、軌跡の紐は原点をぐるぐると囲んでいます。
- 半径 R = 0 のとき、z=0 なので f(z) は定数項 a_0 という一点になります。
もし a_0 \neq 0 であれば、原点を囲んでいた「紐」が、原点を含まない「点」へと縮んでいくことになります。このプロセスにおいて、紐は必ずどこかで原点(0)をまたがなければなりません。 複素平面という「ゴム膜」が原点を包み込み、収縮していく過程で必ず 0 を踏む地点がある。これが、代数的な操作だけでは見えにくい「解の存在」の幾何学的な正体です。
【論理】「初等的な証明」の裏側に隠された前提を解き明かす
代数学の基本定理の証明としてよく紹介されるのが、「|f(z)| の最小値が 0 であることを示す」という手法です。多くの解説記事では「初等的な証明」と謳われますが、実はそこには大学数学で扱う「解析学」の重要なエッセンスが凝縮されています。
なぜ「一番低い地点」が必ず存在するのか?
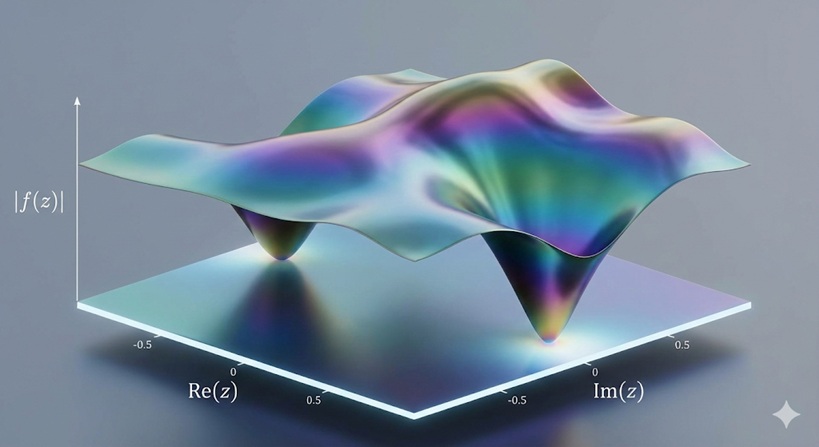
証明の第一歩は、関数 |f(z)| (関数の値の「絶対値」、つまり原点からの距離)に最小値が存在することを確信することです。
変数 z が非常に大きくなると、関数の値 |f(z)| も無限に大きくなります。これを山に見立てると、「遠くへ行けば行くほど標高が無限に高くなる地形」のようなものです。この場合、標高が低い地点を探すために無限の彼方まで探しに行く必要はありません。ある十分に広い「円盤の中」だけを調べれば、その中に必ず「最も標高が低い地点(最小値)」が存在します。
もし「谷底」が 0 でなかったら?(背理法のキモ)
さて、ここからが証明の核心です。「もし、最小値(一番低い地点)の標高が 0 でなかったらどうなるか」を考えます。
仮に、ある点 z_0 で最小値 k > 0 を取ったとしましょう。代数学の基本定理を証明する鍵は、「もし標高が 0 でない場所が最小値だと言い張るなら、そこからさらに少しだけ標高を下げられる方向が必ず見つかる」という事実にあります。
多項式は、その地点 z_0 の周りで非常に柔軟に動きます。複素数の計算を用いると、z_0 からほんの少しだけ適切な方向へ動くことで、|f(z)| の値を k よりも小さくできることが数学的に導かれます。「そこが最小値だ」と決めたのに、さらに低い場所が見つかってしまう矛盾。このロジックが、「最小値は 0 でなければならない」という結論を導き出します。
【歴史】天才たちの「美しい失敗」とガウスの執念

代数学の基本定理は、1799年にカール・フリードリヒ・ガウスが学位論文で証明を与えたことで知られています。しかし、それ以前にもライプニッツやオイラーといった天才たちが「美しい失敗」を繰り返してきました。
ライプニッツが見逃した「複素数の深淵」
17世紀の巨人ライプニッツは、「x^4 + a^4 は、実係数の2次式の積には分解できない」と考え、この定理は成り立たないと誤認していました。実際には実数の範囲で分解可能ですが、彼は複素数が持つ「多項式を分解し尽くす力」を完全には信じ切れていなかったのです。
オイラーの飛躍と、ガウスによる「厳密性」の誕生
18世紀、オイラーも証明を試みましたが、「解があるとするならば、それは a + bi の形をしているはずだ」という前提(循環論法)を置いてしまいました。ガウスはこの点に鋭く切り込み、代数的な計算から「幾何学的な構造の証明」へとパラダイムをシフトさせ、近代数学の扉を開きました。
【実用】「解があるのは分かった。で、どうやって探すのか?」
代数学の基本定理は「解が存在する」ことを保証する存在定理ですが、これは現代のコンピュータが方程式を解くための基盤でもあります。
コンピュータはどうやって「解」を見つけているのか?

5次以上の方程式には代数的な公式がないため、私たちは近似的に解を求める必要があります。ここでワイエルシュトラスの方法(デュラン-カーナー法)といったアルゴリズムが登場します。代数学の基本定理が「n 個の解が必ずどこかにある」と保証してくれているからこそ、コンピュータは迷うことなく、すべての解を見つけ出すまで計算を続けることができるのです。
数学的に「閉じている」ことの圧倒的なメリット
この定理は、「複素数まで広げれば、もうこれ以上新しい数を作る必要はない(代数的閉体)」という終着駅を宣言しました。この数学的な完結さがあるからこそ、私たちは因数分解や行列の固有値、信号処理といった高度な議論を安心して展開できるのです。

まとめ:複素数という「数の終着駅」がもたらす世界
代数学の基本定理は、単なる抽象的な宣言ではありません。
- 幾何学的には:複素平面という「膜」が原点を必ず覆うという連続性の帰結。
- 論理的には:最小値が 0 でなければ矛盾が生じるという、地形の探求。
- 歴史的には:天才たちが到達できなかった「完全な証明」への執念。
この定理を理解することは、数学が一つの巨大で美しい構造体であることを知ることです。次に方程式を解くとき、その解が複素平面という広大な海に必ず存在することを、ぜひ思い出してみてください。



