数学の学習において、「数」の分類を正確に理解することは、方程式や関数といった分野に進むための重要な基礎となります。私たちは直感的に「数」を使っていますが、数学の世界ではその性質によって厳密に分類されています。
この記事では、数学の体系の基本となる「自然数」「整数」「有理数」「実数」「複素数」の5つの数の定義と、それらの関係性について解説します。特に、集合の「包含関係」(どちらがどちらを含むか)に着目し、数がどのように拡張されてきたのかを客観的に整理していきます。この記事を読めば、5つの数の違いと全体の体系が明確になるはずです。
数の体系:5つの数の集合関係(ベン図)
数学で扱う「数」は、その性質に応じて異なる「集合」として分類されます。
私たちが学ぶ5つの主要な数の集合、すなわち自然数(\mathbb{N})、整数(\mathbb{Z})、有理数(\mathbb{Q})、実数(\mathbb{R})、複素数(\mathbb{C})の間には、明確な包含関係(ほうがんかんけい)があります。
包含関係とは、ある集合が別の集合に完全に含まれている状態を指します。5つの数の集合関係は、次のように記号で表すことができます。
\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}これは、「自然数は整数に含まれ、整数は有理数に含まれ…」というように、数が段階的に拡張されていく様子を示しています。
この関係性を視覚的に理解するために、以下のベン図(集合の関係を表す図)を見てみましょう。数がより広い範囲へと拡張されていくイメージが掴めるはずです。
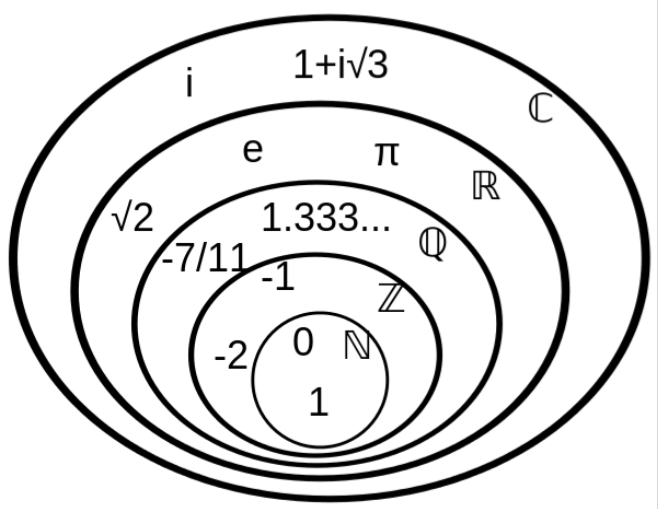
この記事では、この図の外側に向かって、最も基本的な「自然数」から順に、各集合の定義を詳しく見ていきます。
STEP 1. 自然数 (N): すべての始まり
数の体系における最も基本的で直感的な集合が「自然数」です。
自然数の定義
自然数とは、一般に「正の整数」(1, 2, 3, \dots)を指します。ものの個数を数えるために自然発生的に生まれた数であることから、このように呼ばれています。
数学の世界では、自然数の集合を \mathbb{N} という記号で表すことが一般的です。これは、ラテン語の「naturalis(自然な)」の頭文字に由来します。
学習上の注意点:「0」の扱いについて
学習する上で注意が必要なのは「0」の扱いです。
日本の高校数学の教科書においては、0は自然数に含めないことが一般的です。
つまり、 \mathbb{N} = \{1, 2, 3, 4, \dots \} と定義されます。
ただし、学問分野(例えば、大学の集合論やコンピュータサイエンス)や国によっては、0を自然数に含めて \mathbb{N} = \{0, 1, 2, 3, \dots \} と定義する場合もあります。
この記事では、日本の高校数学の標準的な定義に基づき、「自然数は1から始まる正の整数」として解説を進めます。
STEP 2. 整数 (Z): マイナスの世界へ
自然数だけでは、「ない」状態(0)や「不足」している状態(マイナス)を表現できません。そこで数の範囲を拡張したものが「整数」です。
整数の定義
整数とは、自然数(1, 2, 3, \dots)、0、および負の整数(-1, -2, -3, \dots)をすべて合わせた数の集合です。
整数の集合は、ドイツ語の「Zahlen(数)」の頭文字をとって \mathbb{Z} という記号で表されます。
\mathbb{Z} = \{\dots, -3, -2, -1, 0, 1, 2, 3, \dots \}自然数との集合関係 (N ⊂ Z)
ステップ1で定義した自然数(\mathbb{N} = \{1, 2, 3, \dots \})は、すべて整数の集合 \mathbb{Z} に含まれています。
1 や 2 は自然数であり、同時に整数でもあります。
しかし、0 や -1 は整数ですが、自然数ではありません(高校数学の定義による)。
このように、自然数は整数の「部分集合」であるため、\mathbb{N} \subset \mathbb{Z} と表すことができます。
STEP 3. 有理数 (Q): 分数の世界へ
整数だけでは、「1 を 3 で割る」(1 \div 3)のような割り算の結果を正確に表現できません。そこで導入されるのが「有理数」です。
有理数の定義(分数 m/n で表せる数)
有理数とは、2つの整数 m, n(ただし n \neq 0)を使って、分数 \frac{m}{n} の形で表すことができる数の集合です。
例えば、\frac{1}{3} や \frac{-2}{5}、\frac{8}{1} などが有理数です。
有理数の集合は、英語の「Quotient(商)」の頭文字をとって \mathbb{Q} という記号で表されます。割り算の答え(商)として表現できる数、と覚えると分かりやすいでしょう。
整数との集合関係 (Z ⊂ Q)
ステップ2で学んだ整数は、すべて有理数に含まれます。
なぜなら、任意の整数 m は、分母を 1 とすることで \frac{m}{1} という分数で表現できるからです。
例:
- 5 = \frac{5}{1}
- -3 = \frac{-3}{1}
- 0 = \frac{0}{1}
これらはすべて「整数 m, n を使って \frac{m}{n} の形で表せる数」という有理数の定義を満たしています。
整数は有理数に含まれますが、\frac{1}{3} のように有理数であっても整数ではない数が存在します。したがって、\mathbb{Z} \subset \mathbb{Q} という包含関係が成り立ちます。
有理数と小数の関係(有限小数・循環小数)
有理数を小数で表そうとすると、必ず以下の2パターンのどちらかになります。
- 有限小数: \frac{1}{4} = 0.25 のように、途中で終わる小数。
- 循環小数: \frac{1}{3} = 0.333\dots や \frac{1}{7} = 0.142857142857\dots のように、特定の数字の並びが無限に繰り返される小数。
逆に言えば、有限小数や循環小数は、必ず分数(有理数)で表すことができます。
STEP 4. 実数 (R): 無理数の登場
有理数を小数で表すと「有限小数」か「循環小数」になることを学びました。では、循環しない無限小数は存在するのでしょうか。
その答えは「はい」であり、それが「無理数」です。この無理数と有理数を合わせて「実数」と呼びます。
実数の定義(有理数 + 無理数)
実数とは、有理数と無理数を合わせた数の集合です。
実数の集合は、英語の「Real number」から \mathbb{R} という記号で表されます。文字通り「現実に存在する数」といった意味合いがあり、数直線上のすべての点と1対1で対応します。
無理数とは?(循環しない無限小数)
無理数とは、有理数ではない実数のことです。つまり、分数 \frac{m}{n} の形(m, n は整数)で表すことができない数を指します。
無理数を小数で表そうとすると、循環しない無限小数になります。
代表的な無理数には以下のようなものがあります。
- 円周率 (\pi): 3.14159265\dots
- 2の平方根 (\sqrt{2}): 1.41421356\dots
- ネイピア数 (e): 2.71828182\dots
これらはすべて、分数の形で正確に表すことができず、小数で表しても数字の並びが無限に続き、循環することもありません。
有理数との集合関係 (Q ⊂ R)
有理数 (\mathbb{Q}) は、実数 (\mathbb{R}) の一部です。
しかし、上記で挙げた \pi や \sqrt{2} のように、実数ではあるが有理数ではない数(=無理数)も多数存在します。
したがって、有理数は実数の「部分集合」であり、\mathbb{Q} \subset \mathbb{R} という包含関係が成り立ちます。
STEP 5. 複素数 (C): 2乗してマイナスになる世界へ
実数(\mathbb{R})までの範囲では、「2乗してマイナスになる数」は存在しませんでした。例えば、方程式 x^2 = -1 を満たす実数 x はありません。
この問題を解決し、数学の体系をさらに拡張するために導入されるのが「複素数」です。
複素数の定義(実数 + 虚数)
複素数とは、実数 a, b と後述する虚数単位 i を用いて、
a + biという形で表される数の集合です。
a を実部(じつぶ)、b を虚部(きょぶ)と呼びます。
複素数の集合は、英語の「Complex number」から \mathbb{C} という記号で表されます。
虚数単位 i とは?
実数の世界では解けなかった x^2 = -1 という方程式を解くために、数学者たちは新しい「数」を定義しました。それが虚数単位 i です。
虚数単位 i は、
i^2 = -1を満たす数として定義されます。(すなわち、i = \sqrt{-1} です)
この i は実数ではないため、数直線上のどこにも存在しません。
bi(b \neq 0)のように虚数単位 i を含む数を虚数(きょすう)と呼び、実数 a と虚数 bi を組み合わせた a + bi が複素数です。
実数との集合関係 (R ⊂ C)
ステップ4で学んだ実数は、すべて複素数に含まれます。
なぜなら、任意の実数 a は、虚部 b を 0 とすることで a + 0i という複素数の形で表現できるからです。
例:
- 5 = 5 + 0i
- -3.14 = -3.14 + 0i
- \sqrt{2} = \sqrt{2} + 0i
これらはすべて「a + bi の形で表せる数」という複素数の定義を満たしています。
実数は複素数に含まれますが、2 + 3i のように複素数であっても実数ではない数(虚数)が存在します。したがって、\mathbb{R} \subset \mathbb{C} という包含関係が成り立ちます。
なぜ数の世界を拡張するのか?
自然数から複素数へと、なぜこれほど数の世界を拡張する必要があるのでしょうか。
その最大の動機の一つは、「方程式の解を求めるため」です。
- 1. 自然数 (N) のみ
x + 5 = 10 (解: x = 5)は解けますが、x + 5 = 3 は解けません。
- 2. 整数 (Z) へ拡張
x + 5 = 3 (解: x = -2)が解けますが、2x = 3 は解けません。
- 3. 有理数 (Q) へ拡張
2x = 3 (解: x = \frac{3}{2})が解けますが、x^2 = 2 は解けません。
- 4. 実数 (R) へ拡張
x^2 = 2 (解: x = \pm\sqrt{2})が解けますが、x^2 = -1 は解けません。
- 5. 複素数 (C) へ拡張
x^2 = -1 (解: x = \pm i)も解けるようになります。
このように、より複雑な計算や方程式を解けるようにするために、数の概念は拡張され続けてきました。複素数まで拡張することで、高校数学で学ぶ多くの方程式(特に二次方程式)が必ず解を持つようになります。
数の分類に関するFAQ(よくある質問)
Q1. 「0」は自然数に含まれますか?
A1. これは定義によりますが、日本の高校数学の教科書では「0」を自然数に含めないことが一般的です。
自然数は「正の整数」(1, 2, 3, \dots)と定義されます。ただし、学問分野(大学の集合論など)や国によっては 0 を含めて定義することもあるため、文脈の確認が必要です。
Q2. 無理数と有理数の決定的な違いは何ですか?
A2. 決定的な違いは「整数 m, n(n \neq 0)を用いた分数 \frac{m}{n} の形で表せるかどうか」です。
- 有理数: \frac{1}{3} や 5(=\frac{5}{1})のように、必ず分数 \frac{m}{n} の形で表せます。小数にすると「有限小数」または「循環小数」になります。
- 無理数: \pi や \sqrt{2} のように、分数 \frac{m}{n} の形では決して表せません。小数にすると「循環しない無限小数」になります。
Q3. 虚数と複素数は同じものですか?
A3. 同じではありませんが、密接な関係があります。虚数は複素数の一部です。
- 複素数: a + bi(a, b は実数)の形で表される数全体の集合です。
- 虚数: 複素数 a + bi のうち、b \neq 0(虚部が 0 でない)のものです。(例: 2 + 3i, -i)
実数(b=0 の場合)と虚数(b \neq 0 の場合)を合わせたものが複素数全体となります。
まとめ
この記事では、数学の基礎となる5つの主要な数「自然数」「整数」「有理数」「実数」「複素数」の定義と、その関係性について解説しました。
重要なポイントは、これらの数の集合が \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} という「包含関係」にあることです。
最後に、各集合の定義と具体例を一覧表で振り返りましょう。
| 数の種類 | 集合記号 | 定義の概要 | 具体例 |
|---|---|---|---|
| 自然数 | \mathbb{N} | 正の整数 | 1, 2, 100 |
| 整数 | \mathbb{Z} | 自然数、0、負の整数 | -5, 0, 8 |
| 有理数 | \mathbb{Q} | 分数 \frac{m}{n} で表せる数 | \frac{1}{3}, -0.5, 7 |
| 実数 | \mathbb{R} | 有理数と無理数を合わせた数 | \sqrt{2}, \pi, -4, \frac{2}{5} |
| 複素数 | \mathbb{C} | a + bi の形で表せる数 | 2+3i, 5, -i |
数の世界は、方程式の解を求める必要性から、より広く拡張されてきました。これらの分類と体系を理解することが、高校数学を学ぶ上での確かな土台となります。





コメント