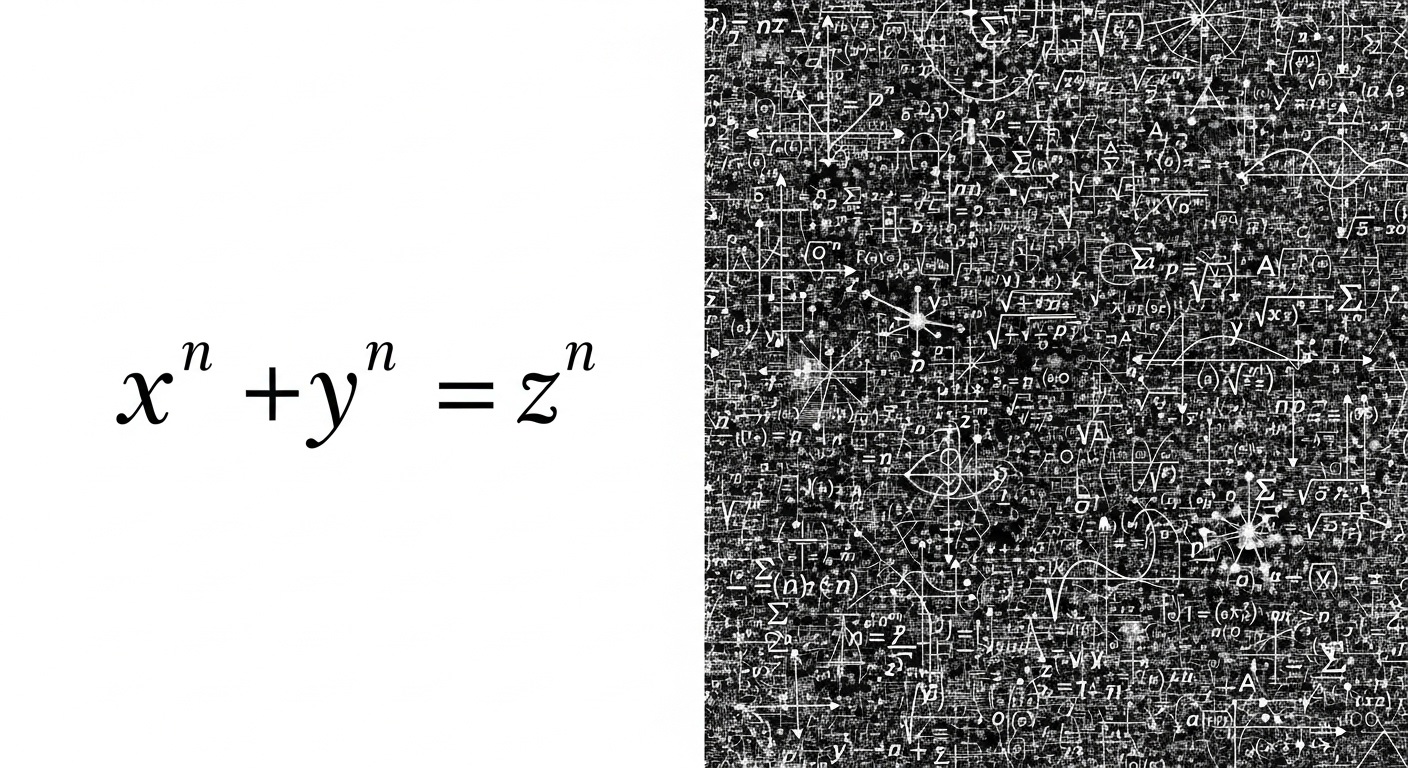フェルマーの最終定理――それは、17世紀の数学者ピエール・ド・フェルマーが提示した、シンプルな見た目とは裏腹に、350年もの間、数多くの数学者を悩ませ続けた難問です。
(n > 2) に整数解は存在しない
というこの定理は、アンドリュー・ワイルズによってついに証明され、数学界に大きな衝撃を与えました。 
この驚くべき業績は、ワイルズ自身の幼少期からの夢と、7年にも及ぶ孤独な研究の末に成し遂げられたものです。本記事では、フェルマーの最終定理の歴史、ワイルズの挑戦、そしてその証明がもたらした数学界への影響を詳しく解説します。
フェルマーの最終定理とは?
17世紀、数学者フェルマーは「において、が3以上の自然数の場合、この等式を満たすゼロでない整数解 は存在しない」という驚くべき予想を残しました。これがフェルマーの最終定理です。非常にシンプルな形のこの定理が、実に350年もの間、世界中の数学者を翻弄することになります。後に「最終定理」と呼ばれる理由や、その歴史については、この後詳しく見ていきましょう。
定理の内容と歴史
フェルマーが約350年前に、古代ギリシャの数学書『算術』の余白に書き残したのがこの定理の始まりです。「を満たす自然数解は、が3以上のときには存在しない」というシンプルな主張でした。彼はその証明について「驚くべき証明を得たが、余白が狭すぎる」と記したのです。このメモが、後の数学者たちにとって最大の挑戦状となったのです。
なぜ「最終定理」と呼ばれるのか
フェルマーは生涯にわたり、数多くの数学的な発見や予想を提示しました。それらの多くは、後の数学者たちによって比較的早い段階で証明されるか、あるいは反例が見つかり解決に至っています。しかし、に関するこの命題だけは、誰にも完全な証明を与えることができませんでした。最後に残された未解決の超難問であったため、「最終定理」と呼ばれるようになったのです。
350年間、多くの数学者が挑んだ難問
フェルマーが「余白がない」として証明を残さなかったこの定理は、その後の数学者たちに計り知れない挑戦を突きつけました。レオンハルト・オイラーをはじめとする歴史に名を刻む偉大な数学者たちが次々と証明に挑みましたが、完全な解決には至りませんでした。350年という長い年月は、この問題の根深い難しさを物語っているといえるでしょう。

過去の偉大な挑戦者たち
350年の歴史の中で、フェルマーの最終定理には多くの数学の巨人たちが挑みました。18世紀にはオイラーがの場合の証明に成功。19世紀にはディリクレとルジャンドルがの場合を、コーシーやラメも取り組みましたが、完全には至りません。特にクンマーは「理想数」の概念を導入し、特定の素数(正則素数)の場合は定理が成り立つことを示しました。彼らの努力は、他の数学分野の発展にも大きく寄与しています。
証明を阻んだ壁
フェルマーの最終定理の証明がこれほど困難だったのは、一見簡単な問題でありながら、当時の数学の枠組みをはるかに超えた概念が必要だったからです。特定のに対する証明は可能でしたが、すべての3以上の自然数について成り立つことを示す普遍的な手法がありませんでした。代数的整数論や、後に登場する楕円曲線といった新しい数学分野の発展を待たねばならなかったのです。
アンドリュー・ワイルズの世紀の挑戦
350年間破られることのなかったフェルマーの最終定理に、一人の数学者が生涯をかけて挑みました。それがイギリスのアンドリュー・ワイルズです。10歳の時にこの定理に出会い、魅せられた少年ワイルズは、いつか必ず証明すると心に誓います。そして、現代数学の力を駆使し、この不朽の難問に立ち向かうことを決意しました。

ワイルズという人物
アンドリュー・ワイルズは1953年生まれのイギリスの数学者です。彼のフェルマーの最終定理への挑戦は、10歳の時に図書館でこの問題に出会ったことから始まります。そのシンプルさと歴史的な背景に強く惹きつけられ、彼は生涯をかけてこの定理を証明することを心に誓いました。整数論を専門とする数学者として、この少年時代の夢を追い続けることになります。
7年間に及ぶ秘密の研究
ワイルズはフェルマーの最終定理の証明を、他の研究から離れて7年間、秘密裏に進めました。その鍵となったのが、日本の数学者である谷山豊、志村五郎が提唱した「谷山・志村予想」(現モジュラー性定理)です。この予想とフェルマーの最終定理の間に驚くべき繋がりがあることを知ったワイルズは、この現代数学の難問に取り組むことで、最終定理の証明を目指しました。孤独な研究室での、長く厳しい道のりでした。
一度の挫折、そして完全な証明へ
1993年、ワイルズはケンブリッジで証明を発表し、世界中の数学者から賞賛を浴びました。しかし、その後の査読で証明にごくわずかな、しかし致命的な誤りが見つかります。長年の努力が水泡に帰すかに見えましたが、ワイルズは諦めませんでした。かつての教え子リチャード・テイラーと共に1年以上もの間、困難な修正作業に取り組み、1994年にようやく完全な証明を完成させたのです。この瞬間、350年の歴史に終止符が打たれたのでした。
証明達成の意義と影響
アンドリュー・ワイルズによるフェルマーの最終定理の証明は、単なる一つの定理の解決にとどまらず、数学界に計り知れない影響を与えました。350年もの間、多くの数学者を苦悩させた問題に終止符が打たれたことは、数学史における記念碑的な出来事です。特に、谷山・志村予想の重要性が改めて認識され、整数論と幾何学を結びつける新しい時代の幕開けを告げるものとなりました。

数学界にもたらされた衝撃
ワイルズの証明は、長らく未解決だったフェルマーの最終定理に終止符を打っただけでなく、数学界に大きな衝撃と影響を与えました。特に、証明に使われた「谷山・志村予想」が、整数論と楕円曲線という、それまで一見無関係だった分野を繋ぐ極めて重要なものであることが証明された意義は大きいです。これにより、数学の異なる領域間の連携が深まり、新たな研究方向が開かれました。
ワイルズが残した功績
アンドリュー・ワイルズの最大の功績は、もちろんフェルマーの最終定理を証明したことです。この偉業に対し、彼は数学のノーベル賞と称されるフィールズ賞の特別賞(規定の40歳を超えていたため)、アーベル賞など、数多くの栄誉ある賞を受賞しました。彼の証明は、新たな数学的手法を開拓し、特に谷山・志村予想を定理へと昇華させた意義は大きいです。ワイルズの粘り強い挑戦は、次世代の数学者にも大きなインスピレーションを与えています。
まとめ
フェルマーが350年前に残したシンプルな問いは、多くの数学者たちの想像力を掻き立て、挑戦の歴史を紡ぎました。アンドリュー・ワイルズによる証明は、この長きにわたる探求に終止符を打ち、数学史における不朽の金字塔となりました。彼の粘り強い努力と、谷山・志村予想といった現代数学の力を結集したこの偉業は、数学の異なる分野を結びつけ、新たな時代の研究に深い影響を与えています。フェルマーの最終定理の物語は、数学の未解決問題が人類の知的好奇心を刺激し、分野全体の発展を推進する力となることを示しています。