フィボナッチ数列や黄金比という言葉を、一度は耳にしたことがあるかもしれませんね。実はこれらの数字の並びや比率は、私たちのすぐそばにある自然の造形から、歴史を彩る芸術作品、そして現代社会の金融市場を分析するツールに至るまで、驚くほど多くの場面でその不思議な姿を現します。この記事では、そんな奥深くも魅力的なフィボナッチ数列と黄金比の謎に迫ります。基本的な性質から、あっと驚くような出現例、さらには意外な分野での応用方法まで、分かりやすく解き明かしていきましょう。読み終える頃には、あなたが世界を見る目が少し変わるかもしれません。
フィボナッチ数列とは? – 謎解きの第一歩

「ウサギの増え方」から発見?フィボナッチ数列の面白い起源
この不思議な数列、実は「ウサギのつがいがどれくらい増える?」という問いから見出されました。13世紀イタリアの数学者レオナルド・フィボナッチが自身の著書『算盤の書』で紹介したのです。特定の条件下でウサギが子どもを産むと仮定すると、その総数がこの数列に従って増えていくという、興味深いエピソードです。
シンプルだけど奥深い!フィボナッチ数列の基本的なルール
フィボナッチ数列のルールは驚くほど単純。最初の2つの数を0と1とすると、あとは「直前の2つの数を足す」という作業を繰り返すだけです。つまり、0, 1, 1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3)…と続いていきます。このシンプルな規則から、実に多様な現象が説明できるのは驚きですね。
不思議な一致?フィボナッチ数列と「黄金比」の密接な関係
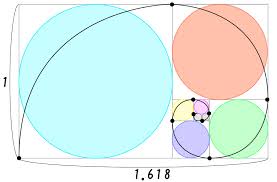
フィボナッチ数列の隣り合う2つの数を取り出し、大きい方を小さい方で割ってみてください。例えば5を3で割ると約1.666。数列の項が進むにつれて、この比率はある特定の値、約1.618へと近づいていきます。これこそが古くから「最も美しい比率」とされる「黄金比」。数列と比率、二つの数学的な概念の間に見られるこの不思議なつながりは、多くの人々を魅了してきました。
自然界に隠されたフィボナッチ数列と黄金比のパターン

花びらの枚数や松ぼっくりに潜む「美」の法則
身近な自然に目を向けると、そこにもフィボナッチ数が隠れています。例えば、以下のように多くの植物でフィボナッチ数が見られます。
- ユリ、アヤメ:3枚
- サクラ、ウメ、キンポウゲ:5枚
- コスモス、デルフィニウム:8枚 これらはフィボナッチ数そのものです。また、松ぼっくりの鱗(うろこ)が描く螺旋の数も、フィボナッチ数になっていることが多いのをご存知でしたか。まるで植物が数学を知っているかのようです。
ヒマワリの種の並びにも!植物が知る驚きの数学
夏の太陽に向かって力強く咲くヒマワリ。その中心部をよく観察すると、種が螺旋状にぎっしりと並んでいるのが分かります。実はこの螺旋、右回りと左回りのそれぞれの数が、多くの場合フィボナッチ数になっているのです(例えば34と55など)。これは種を効率よく配置し、太陽光や栄養を最大限に得るための、自然が編み出した驚くべき数学的設計と考えられています。
オウムガイから台風の渦まで?壮大な自然現象とのつながり
フィボナッチ数列と深く関連する「黄金螺旋」という形は、オウムガイの殻が描く美しいカーブにも見られます。成長するにつれて、巻き貝が一定の比率を保ちながら大きくなっていく様は、まさに自然の造形美。さらには、台風の渦巻きや遠い銀河の腕の形など、より壮大なスケールの現象にも同様のパターンが見いだされることがあります。
人類を魅了するアートとデザインの中のフィボナッチ

歴史的建造物や名画に見る、心地よい「黄金比」の構図
古くから人々を魅了し続けてきた芸術作品や歴史的建造物にも、黄金比は頻繁にその姿を見せます。例えば、古代ギリシャのパルテノン神殿や、レオナルド・ダ・ヴィンチの「モナ・リザ」といった数々の名作に、その比率が巧みに用いられていると言われています。この比率こそが、私たちに無意識の安定感や調和の取れた心地よさを感じさせているのかもしれません。
音楽のリズムや詩にも?フィボナッチ数列が奏でるハーモニー
美の追求は、視覚芸術の世界だけに留まりません。クラシック音楽に目を向ければ、モーツァルトやバルトークといった偉大な作曲家たちが、楽曲の構成要素や小節の展開にフィボナッチ数列を取り入れたとされる例があります。現代音楽や詩の世界でも、リズムや音節の数にこの数列を応用し、独特の心地よさや高揚感を生み出す試みが見られることも。あなたの好きなあの曲にも、フィボナッチが隠れているかもしれません。
ロゴデザインやウェブレイアウトにも活かされる美の法則
私たちが日常的に目にしている企業のロゴマークや、ウェブサイトのデザインにも、フィボナッチ数列や黄金比の考え方が活かされています。構成要素の配置バランスやサイズの比率にこれらの「美の法則」を取り入れることで、視覚的に調和が取れ、多くの人にとって心地よく感じるデザインを生み出すことが可能になるのです。何気なく見ているあのロゴも、実は計算された美しさなのかもしれません。
金融から最先端技術まで!フィボナッチ数列の多彩な応用

【トレーダー必見】市場の動きを読む?フィボナッチ・リトレースメントとは
金融市場の価格分析、特にテクニカル分析という分野では「フィボナッチ・リトレースメント」が広く知られています。これは株価や為替レートなどの価格が大きく動いた後、一時的な反発や反落がどの程度の水準まで起こりやすいかを予測しようとする手法の一つ。フィボナッチ数列から導かれる以下の特定の比率が、重要な支持線や抵抗線の目安として市場参加者に意識されることがあります。
- 23.6%
- 38.2%
- 61.8%
コンピュータ科学を支えるフィボナッチ数列のアルゴリズム
私たちの目に見えない情報技術の世界でも、フィボナッチ数列は重要な役割を担っています。コンピュータ科学の分野では、大量のデータの中から目的の情報を効率的に見つけ出す検索アルゴリズム(フィボナッチ探索)や、複雑な処理をより速く行うためのデータ構造(フィボナッチヒープ)などに応用されているのです。さらには、情報を安全に保護するための暗号技術にも、この数列のユニークな性質が利用されることがあるのは非常に興味深い点です。
【受験生・高校生向け】数学の問題解決にも役立つフィボナッチ的思考
数学の問題、特に場合の数や数列の規則性を見つけ出すような場面で、フィボナッチ数列の考え方が思わぬ形で役立つことがあります。
例えば「階段を1段ずつ、または2段ずつで上る場合、n段上る方法は何通りあるか?」といった問題。
実は、この問題の答えとなる上り方の総数は、フィボナッチ数列の考え方を使って見事に求められるのです。「1つ前と2つ前の状態に着目して考える」という視点は、様々な問題解決のヒントになるでしょう。
もっと深く知りたい!フィボナッチと黄金比の面白トリビア
あらゆる整数を表現?「ゼッケンドルフの定理」とは
フィボナッチ数列には「ゼッケンドルフの定理」という、少々変わった面白い性質があります。これは、どんな正の整数でも「連続しないフィボナッチ数」(ただし最初のF1=1は除く場合が多い)の和として、ただ一通りに表すことができるというもの。例えば、17という数は、13 (F7) + 3 (F4) + 1 (F2) のように分解できます。まるで数字の秘密の組み合わせパズルのようですね。
フィボナッチ数列専門の学術誌があるってホント?
これは驚かれるかもしれませんが、フィボナッチ数列だけを専門的に扱う学術雑誌が実際に存在します。その名も「Fibonacci Quarterly」。1963年の創刊以来、今日に至るまで、世界中の数学者や熱心な研究者たちが、このシンプルな数列に関する新しい発見や応用例についての学術論文を発表し続けているのです。
一つの数列がこれほどまでに深く、そして長く探求され続けるとは、その奥深さを物語っています。
有名アーティストも取り入れた?楽曲に隠されたフィボナッチ
フィボナッチ数列は、思いもよらない形で現代の音楽シーンにも影響を与えています。
例えば、アメリカの著名なプログレッシブ・メタルバンド「Tool」の楽曲「Lateralus」には、歌詞の音節数がフィボナッチ数列の順序に従って巧みに構成されているセクションがあるのです。
このように意図的に数理的なパターンを楽曲の構造に取り込むとは、実に独創的で知的な試みと言えるでしょう。
フィボナッチ数列と黄金比 – 終わらない探求と無限の可能性
フィボナッチ数列と黄金比の世界、その奥深さに少しでも触れていただけたでしょうか。
ウサギの計算という可愛らしい問題から始まり、自然界の息をのむような美しいパターン、時代を超える芸術作品の普遍的な構図、さらには現代の金融市場の動向分析に至るまで、その影響は計り知れません。
この不思議な数列と比率は、私たちの尽きない知的好奇心を刺激し、世界を新たな視点から眺めることの面白さを教えてくれます。
この記事が、皆さんの学びや日々の探求心をさらに深めるための一つのきっかけとなれば幸いです。数学や自然の法則の中には、私たちがまだ知らない面白い発見が、きっとまだまだ隠されていることでしょう。