学校のクラスで23人集まったとき、同じ誕生日のペアがいる確率はどのくらいだと思いますか?
直感的には「数パーセントくらいかな?」と感じるかもしれません。
しかし、実は「その場にいる誰かと誰かが同じ誕生日である確率」は50%を超えます。
これは「誕生日のパラドックス」と呼ばれる有名な数学の確率問題です。なぜ人間の直感はこれほど外れるのでしょうか?
この記事では、サッカーの試合や数式を使って、その不思議な仕組みを分かりやすく解説します。読み終わる頃には、直感のズレがスッキリ解消されているはずです。
誕生日のパラドックスとは?23人で50%を超える不思議
サッカーの試合(23人)で想像してみよう
まずは、イメージしやすい「サッカーの試合」で考えてみましょう。
ピッチ上には、両チームのイレブン(11人×2)と主審(1人)の合計23人がいます。

キックオフの笛が鳴るその瞬間、ピッチ上の23人の中に「同じ誕生日のペア」がいる確率は、なんと約50.7%。
つまり、2回に1回は同じ誕生日の二人がグラウンドに立っている計算になります。
「そんなに高いはずがない!」と感じるのが普通です。しかし、数学的な計算をすると、この驚きの数字が真実であることが証明されます。
なぜ直感とズレるのか?「視点」の違いを解説
「私と同じ」vs「誰かと誰かが同じ」
多くの人が「23人しかいないのに確率が高すぎる」と感じるのは、無意識に「自分と同じ誕生日の人がいる確率」を想像してしまうからです。
「自分」対「残りの22人」。この場合、自分と同じ誕生日の人がいる確率は確かに低く、約6%しかありません。
しかし、誕生日のパラドックスで問われているのは、「その場にいる誰かと誰か」が同じである確率です。
AさんとBさん、CさんとDさん、あるいは先生とAさん……。「自分」を含まないペアも含めて、クラス全体のあらゆる組み合わせが対象になります。
主役は「ペアの数」:23人で253通り!
では、23人のクラスには、全部で何通りのペア(組み合わせ)があるのでしょうか?
これは、23人全員で総当たり戦のジャンケンをしたり、お互いに握手をする回数を計算するのと同じです。
異なるn個のものからr個を選ぶ組み合わせの数は、数学記号で {}_nC_r と書きます。
今回の「23人から2人のペアを作る」計算は、以下のようになります。
なんと、たった23人に見えても、その中には253通りものペアが存在するのです。

「23回」のチャンスだと思ったら、実は「253回」もチャンス(判定回数)があったわけです。
これだけの回数があれば、その中に「誕生日が一緒」というペアが1組くらい見つかっても不思議ではない気がしてきませんか?
これが、直感(人数)と事実(ペアの数)のズレの正体です。
【検証】人数ごとの確率推移と「自分と同じ」確率
確率一覧表(10人〜50人)
では、人数が増えるにつれて、確率はどのように変化していくのでしょうか。
分かりやすく表にまとめました。23人を境に一気に確率が上がっていく様子が分かります。
| 人数 | 同じ誕生日の組がいる確率 | 備考 |
|---|---|---|
| 10人 | 約 11.7% | まだ低い |
| 20人 | 約 41.1% | かなり高くなってきた |
| 23人 | 約 50.7% | ここで50%を超える! |
| 30人 | 約 70.6% | 驚くほど高い |
| 40人 | 約 89.1% | ほぼ間違いなくいる |
| 50人 | 約 97.0% | いない方が珍しい |
| 60人 | 約 99.4% | ほぼ100% |
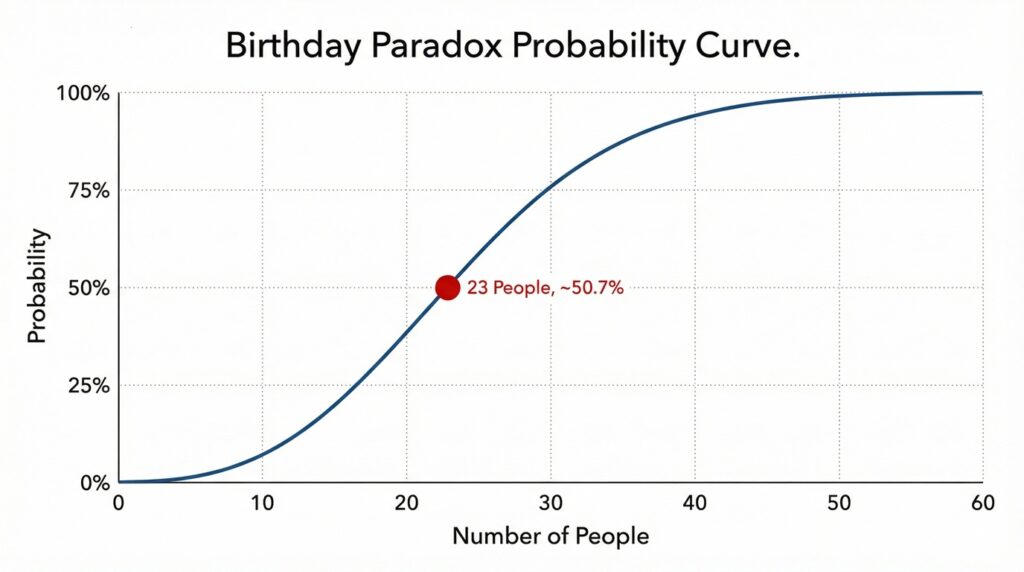
驚くべきことに、学校の1クラス(約30〜40人)であれば、70〜90%近い確率で同じ誕生日のペアが存在することになります。
さらに、60人もいれば確率は99%を超えます。 100人集める必要すらないのです。
【コラム】「自分と同じ」誕生日を見つけるには253人必要
ここで、多くの人が最初に抱いた「直感」についても触れておきましょう。
「クラスの中で、私と同じ誕生日の人はいるか?」という疑問です。
この場合、対象は「自分 vs 他のみんな」という特定の関係になるため、ペアの組み合わせ数はガクンと減ります。
計算すると、自分と同じ誕生日の人がいる確率が50%を超えるには、なんと253人も必要になります。
- 誰かと誰か(パラドックス): たった23人でOK
- 特定の誰か(自分): 253人も必要
この「条件の違い」こそが、誕生日のパラドックスが不思議に感じる最大の理由なのです。
【理論】確率50%を超える計算式とExcel活用法
「余事象」で計算する(1引く「全員バラバラ」)
「少なくとも1組のペアがいる確率」を直接計算するのは、実はとても大変です。「AさんとBさんが同じ」「BさんとCさんが同じ」「3人が同じ」……と、パターンが膨大すぎるからです。
そこで、数学の便利なテクニック「余事象(よじしょう)」を使います。
ある事象Aに対して、「Aが起こらない」という事象のこと。
全確率(100% = 1)から、「Aが起こらない確率」を引けば、「Aが起こる確率」が求められます。
式: 確率 = 1 – (逆のパターンの確率)
今回の場合は、こう考えます。
「少なくとも1組いる確率」 = 1 - 「全員の誕生日がバラバラの確率」
「全員バラバラ」の確率は、次のように一人ずつ順番に考えていくと計算できます。
- 1人目: 誰とも被らない(確率 365/365 = 100%)
- 2人目: 1人目と違う日ならOK(確率 364/365)
- 3人目: 1,2人目と違う日ならOK(確率 363/365)
- …
- 23人目: 前の22人と違う日ならOK(確率 343/365)
これを全員分掛け合わせると、「23人全員がバラバラの確率」は約49.3%になります。
最後にこれを1(100%)から引きます。
1 - 0.493 = 0.507
つまり、50.7%。これが「少なくとも1組ペアがいる確率」の正体です。
Excel関数でシミュレーションしてみよう
この計算は、Excel(エクセル)などの表計算ソフトを使えば一瞬で確かめることができます。
興味のある人は、空いているセルに以下の数式をコピー&ペーストしてみてください。
=1-(PERMUT(365,23)/365^23)
PERMUT(365,23):365日の中から23人の誕生日が全員異なる順列の数365^23:23人の誕生日の全パターン(重複あり)
エンターキーを押すと、「0.507…」という数字が表示されるはずです。
数字の「23」の部分を「40」や「50」に変えてみると、確率がどう変化するかすぐに実験できますよ。
【応用】この知識はどこで役に立つ?
単なる計算遊びのように思える「誕生日のパラドックス」ですが、実は私たちの個人情報やセキュリティを守る技術にも応用されています。
情報セキュリティへの応用(ハッシュ衝突)
インターネット上の暗号技術では、パスワードやデータを「ハッシュ値」という適当な文字列(デジタルな指紋のようなもの)に変換して管理しています。
本来、異なるデータからは異なるハッシュ値が生まれるはずですが、偶然同じ値になってしまうことを「衝突(コリジョン)」と呼びます。
ハッシュ値の桁数が一見十分に多く見えても、誕生日のパラドックスと同じ理屈で、意外と少ない試行回数で「衝突」が見つかってしまう脆弱性のこと。
これを防ぐために、現代の暗号技術(SHA-256など)は、天文学的な回数の計算をしないと衝突しないように設計されています。
「直感よりも衝突確率は高い」という数学的事実は、ハッカーからシステムを守るための重要な教訓になっているのです。
現実世界のバイアス(季節性)の影響
ちなみに、実際の人間社会では、誕生日は365日均等には分布していません。
国や地域によって、「9月生まれが多い」「年末年始は少ない」といった偏り(バイアス)があります。
数学的には、「偏りがあるほど、衝突する(被る)確率は高くなる」という性質があります。
つまり、現実のクラスや職場では、計算上の50.7%よりも、さらに高い確率で同じ誕生日のペアが見つかる可能性が高いのです。
誕生日のパラドックスに関するよくある質問(FAQ)
A. 厳密に計算に入れると非常に複雑になりますが、全体の確率への影響は誤差レベル(0.1%未満)です。通常は365日で計算するか、366日として計算しても結果はほぼ変わりません。
A. 367人です。
1年は最大366日(うるう年含む)なので、それより1人多い367人が集まれば、「鳩の巣原理」により、理屈上必ず誰かと誰かが同じ誕生日になります。
まとめ:確率は人間の直感を裏切る
記事のポイントをまとめます。
- 23人いれば、同じ誕生日のペアがいる確率は50%を超える。
- 理由は、23人の背後にある「253通りのペア」が確率を押し上げているから。
- 「自分と同じ」人を探すには253人必要だが、「誰かと誰か」なら23人で十分。
人間の直感は、確率に関してはあまり当てになりません。
次に学校や職場の飲み会などで20人以上集まる機会があれば、ぜひ「この中に同じ誕生日のペアがいるか?」を調べてみてください。
きっと、数学の不思議をリアルに体験できるはずです。





コメント