「三平方の定理(ピタゴラスの定理)」という言葉、学生時代に耳にしたことがあるのではないでしょうか。
「a²+b²=c²…なんとなく見覚えはあるけど、どういう意味?」
「これって実生活で何の役に立つの?」
そう感じている方も少なくないかもしれません。
実は、三平方の定理は私たちの身の回りにあふれています。 地図アプリのルート計算、テレビ画面の大きさの秘密、人気ゲームのプログラムの中にも、この定理が活用されているのです。
この記事では、三平方の定理の基本から、あっと驚く身近な使い方、「なぜ?」がわかる簡単な証明、面白い歴史までを丁寧に解説します。 読み終える頃には、数学のイメージが「面白い!」に変わっているはずです。
三平方の定理とは?まずは基本の公式を分かりやすく解説
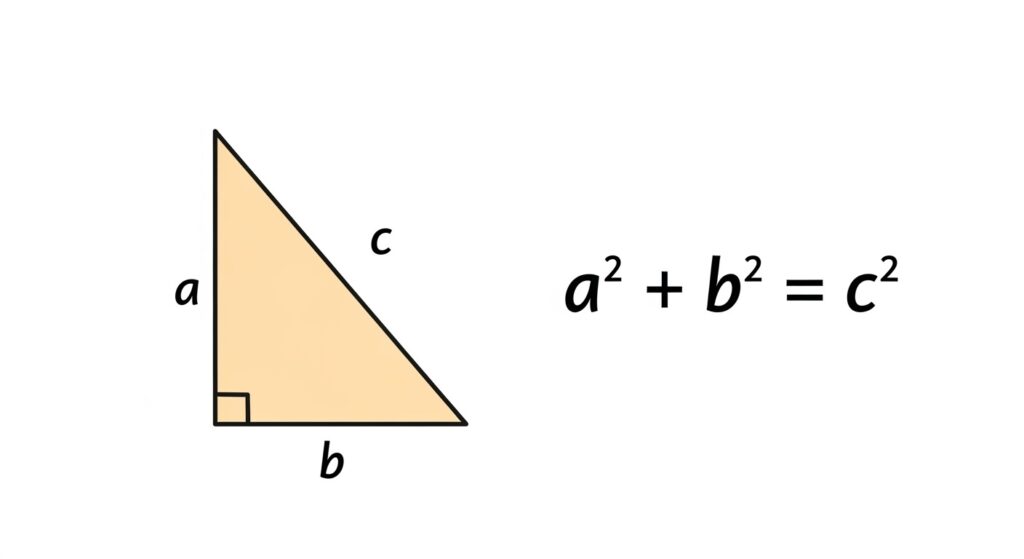
「直角三角形」の3辺の関係を示す魔法の公式
三平方の定理は、直角三角形の3つの辺の長さに関する、とてもシンプルな法則です。
直角をはさむ2つの短い辺の長さをそれぞれ「a」と「b」、そして最も長い斜辺の長さを「c」とすると、
「a²+b²=c²」
という式が必ず成り立ちます。²は同じ数を2回かける「2乗」という意味です。
覚えておくと計算が楽になる「ピタゴラス数」とは?
ピタゴラス数とは、三平方の定理の式をぴったり成り立たせる、3つの整数の組み合わせのことです。
最も有名なのが「3, 4, 5」の組。 実際に計算すると 3² + 4² = 9 + 16 = 25 となり、5² = 25 と一致します。
他にも次のような組み合わせがあり、これを覚えておくと計算がとても楽になりますよ。
【一番知りたい】三平方の定理の身近な使い方7選
それでは、この定理が私たちの生活でどのように役立っているのか、7つの身近な例を見ていきましょう。
- テレビ・スマホ画面の「インチ」の謎
- 地図アプリの距離計算
- DIYや部屋の模様替えでの「直角」出し
- 野球のダイヤモンドの距離
- GPSの仕組み
- ゲームキャラクターの動き
- 高い木の高さの測定
テレビ・スマホ画面の「インチ」の謎が解ける
テレビやスマホの「50インチ」といったサイズは、実は画面の対角線の長さを示しています。
でも、本当に知りたいのは縦と横の長さですよね。 画面の縦横比(多くは16:9)が分かっていれば、三平方の定理を使って「縦² + 横² = 対角線²」から、実際の縦と横の長さを計算することができるのです。
地図アプリはどうやって距離を計算している?
スマホの地図アプリで距離が表示されるのも、三平方の定理のおかげです。
アプリは、2つの地点の緯度と経度の差を、直角三角形の縦と横の辺に見立てます。 そして、求めたい2地点間の直線距離を斜辺として計算しているのです。
実際の道順は複雑ですが、基本的な距離計算にはこの原理が使われています。
DIYや部屋の模様替えで「直角」を出す方法
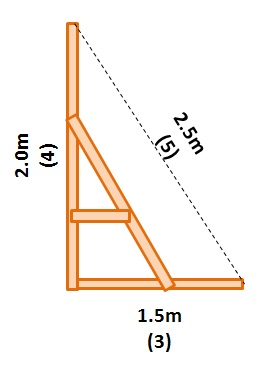
DIYで棚を作ったり、家具を配置したりする時、正確な直角を出したい場面はありませんか?
そんな時に、あの「3, 4, 5」のピタゴラス数が役立ちます。 メジャーを使い、角から片方に30cm、もう片方に40cmの印をつけ、その2点間が50cmになれば、その角は完璧な90度。プロの大工さんも使うテクニックです。
野球のダイヤモンドは美しい直角三角形
野球のグラウンドにも三平方の定理が隠されています。 ホームから1塁、1塁から2塁はそれぞれ約27.4m。
ではキャッチャーが2塁へ盗塁を阻止する時の送球距離は? これはホームと1塁、1塁と2塁を辺とする直角三角形の斜辺にあたります。定理で計算すると、約38.7mになることがわかります。
あなたのいる場所もわかる?GPSの仕組み
今いる場所を教えてくれるGPSも、三平方の定理が応用されています。 GPSは複数の人工衛星からの距離を基に現在地を特定します。
衛星と自分との距離を斜辺とし、地上の位置(緯度・経度)との関係を計算するのです。 3つ以上の衛星からの距離が分かれば、地上での正確な2次元の位置が特定できる、という仕組みです。
ゲームの世界でもキャラクターは計算して動いている
テレビゲームの世界でも三平方の定理は大活躍。 キャラクターや敵の位置は、画面上のX座標とY座標で管理されています。
2つのキャラクター間の距離を測る時、それぞれのX座標の差とY座標の差を2辺とする直角三角形を考えます。 その斜辺の長さを定理で計算し、当たり判定などに利用しているのです。
高い木の根元から離れて見上げると…?
直接は登れない高い木の高さも、三平方の定理で推定できます。
まず、木から少し離れた場所に立ちます。 すると「木と地面の距離」「自分の目線から木のてっぺんまでの高さ」「自分と木のてっぺんを結ぶ直線」で直角三角形ができます。 このうち2つの辺の長さが分かれば、残りの辺の長さ、つまり木の高さも計算できるのです。
なぜ?を解決!三平方の定理のやさしい証明
パズルみたいで面白い!図形を並べ替える証明
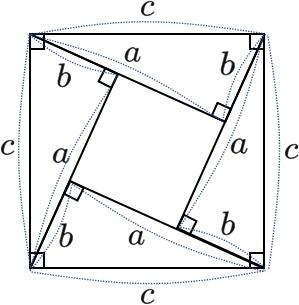
「なぜ?」を解決する、まるでパズルのような証明方法があります。
まず、同じ形の直角三角形を4つ用意します。 これをうまく並べ替えると、斜辺cを1辺とする大きな正方形を作ることができます。
この正方形の面積は c² ですが、これは元の三角形4つと小さなすき間の面積の合計と同じです。 この関係から「a²+b²=c²」が導き出せるのです。
もっと知りたい人へ:相似を使った証明
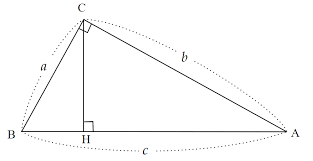
もう少し数学的な証明に挑戦したい人には、相似を利用する方法もおすすめです。
まず、大きな直角三角形の直角の頂点から、斜辺に向かって垂線を引きます。 すると、大きさの違う3つの相似な三角形が現れます。
これらの辺の比が等しいことを利用して計算していくと、驚くほどスッキリと「a²+b²=c²」を導くことができます。
ちょっと寄り道。三平方の定理の面白い歴史

発見者はピタゴラスじゃない?古代からの知恵
この定理はピタゴラスの名を冠していますが、彼が最初に発見したわけではありません。
実は、ピタゴラスが生まれる1000年以上も前の古代バビロニアでは、すでにこの法則が知られ、土地の測量や建築に活用されていたのです。 エジプトのピラミッド建設にも使われたという説もある、まさに古代からの知恵なのです。
なぜ「ピタゴラスの定理」と呼ばれているの?
最初の発見者ではないのになぜ「ピタゴラスの定理」?
それは、彼がこの法則に「なぜそうなるのか?」という数学的な証明を初めて与えた人物だと考えられているからです。 それまでの人々が経験的に「使える」と知っていたものを、ピタゴラスは「いつでも成り立つ真理(定理)」として、その価値を大きく高めたのです。 その功績から彼の名で呼ばれるようになりました。
まとめ:三平方の定理は世界の見方を変える面白いツール
三平方の定理について、基本の公式から身近な応用例、簡単な証明、そして面白い歴史までをご紹介しました。 「a²+b²=c²」というシンプルな式が、地図アプリからゲームの世界まで、こんなにも多くの場面で役立っていることに驚かれたのではないでしょうか。
この定理は、ただの暗記する公式ではありません。 世界の図形的な性質を解き明かすための、強力で面白いツールなのです。
この記事を通して、これまで「難しい」「役に立たない」と感じていた数学のイメージが、少しでも「身近で面白いかも」に変わっていれば幸いです。
にほんブログ村(算数・数学科教育)




