「素数」と聞くと、学生時代に習った懐かしい言葉だと感じるかもしれません。しかし!、素数は単なる数字のパズルではなく、現代のインターネット社会を根底から支える、極めて重要な存在です。
この記事では、素数の基本的な意味から、その面白い種類、そして私たちの安全を守る暗号技術との驚くべき関係まで、その不思議な世界のすべてを分かりやすく解き明かしていきます。
そもそも素数とは?【基本のキ】
数学の世界には、すべての数の「もと」となる、とても重要な数字が存在します。
それが「素数」です。
ここでは、その基本的な定義から、多くの人が疑問に思うポイントまで、一つずつ丁寧に見ていきましょう。
素数の定義:「1」と「自分自身」でしか割り切れない数
素数とは、「1」と「その数自身」の2つしか約数を持たない、1より大きい自然数のことです。
約数
言葉だけだと少し難しく感じるかもしれませんね。
具体例を見てみましょう。
- 「7」は、1と7でしか割り切れません。なので素数です。
- 「13」も、1と13でしか割り切れないため、素数です。
- 一方「6」はどうでしょう。1と6以外にも、2や3で割り切れてしまいます。そのため、6は素数ではありません。
このように、割り切れる数が2つだけに限定されている、いわば「孤高の数字」が素数なのです。

なぜ「1」は素数ではないの?多くの人がつまずくポイントを解説
「1も、1と自分自身でしか割り切れないのでは?」
これは、素数を学ぶときに誰もが一度は通る疑問です。
結論から言うと、1は素数ではありません。
その理由は、素数の定義をより厳密に「約数がちょうど2つある自然数」としているからです。
「1」の約数は「1」の一つしかありません。
約数が2つではないため、素数の仲間には入れない、というわけです。
このルールがあることで、後述する「算術の基本定理」が美しく成り立ちます。
素数と合成数、兄弟のような関係
1より大きい自然数は、素数と、もう一つ「合成数」という数に分けることができます。
合成数とは、素数の逆で「1とその数自身以外にも約数を持つ数」のことです。
先ほど例に出した「6」や、「9」(1, 3, 9で割り切れる)、「12」(1, 2, 3, 4, 6, 12で割り切れる)などが合成数にあたります。
つまり、1を除いたすべての自然数は、素数か合成数のどちらかに分類される関係なのです。
すべての数は素数でできている?「算術の基本定理」
素数が「数の原子」と呼ばれる、非常に重要な理由があります。
それが、「算術の基本定理」という数学の基本的なルールです。
これは、すべての合成数は、素数の掛け算の形に分解できるという定理。
しかも、その組み合わせはただ一通りしかありません。
例えば、「60」という数を分解してみましょう。
60 = 2 × 2 × 3 × 5
このように、「60」は「2」という素数2個、「3」という素数1個、「5」という素数1個の掛け算で作られています。
他のどんな素数の組み合わせを使っても、60を作ることはできません。
この性質が、素数がすべての数の根源であるといわれる所以です。
まずは探してみよう!素数一覧と簡単な見分け方
素数の定義がわかったところで、次は実際にどんな数字が素数なのかを見ていきましょう。
「この数字、素数かな?」と思ったときに、自分で見分けられる簡単な方法も紹介します。
【100まで】素数一覧表
まずは、比較的身近な1から100までの数字の中に、素数がいくつあるのか見ていきましょう。
全部で25個あります。
| 2 | 3 | 5 | 7 | 11 |
| 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 |
| 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 |
こうして見ると、数字が大きくなるにつれて素数が現れる間隔が広がっていくなど、不規則に並んでいる様子が分かりますね。
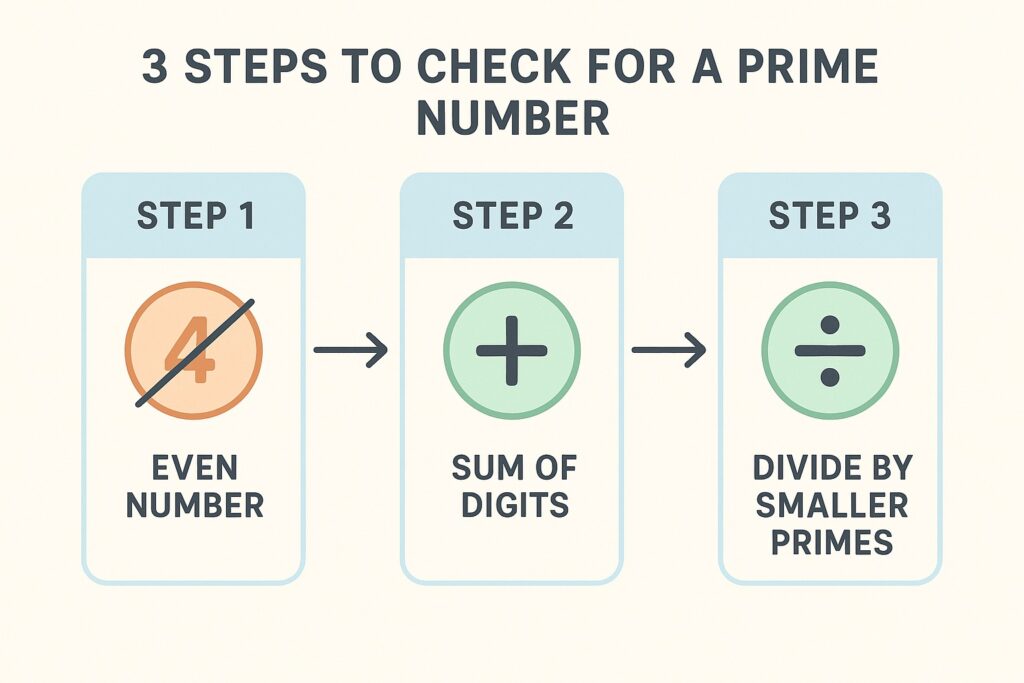
これで迷わない!素数かどうかを判定する3つのステップ
100より大きい数字が素数かどうかを知りたいとき、簡単なステップで判定することができます。
ここでは例として「113」が素数かどうかを調べてみましょう。
ステップ1:偶数と5の倍数を除外する
まず、最も簡単なチェックです。
- 「2」以外の偶数(一の位が0, 2, 4, 6, 8)は、すべて2で割り切れるので素数ではありません。
- 「5」以外の5の倍数(一の位が0, 5)は、すべて5で割り切れるので素数ではありません。
「113」は一の位が「3」なので、このステップはクリアです。
ステップ2:各位の和が「3の倍数」かチェックする
次に、3で割り切れるかを確認します。これには簡単な裏技があります。
数字の各位を足し算し、その答えが3の倍数なら、元の数字も3の倍数になります。
- 例:「111」→ 1 + 1 + 1 = 3。3は3の倍数なので、111も3で割り切れます。
「113」の場合は、1 + 1 + 3 = 5。5は3の倍数ではないので、3では割り切れません。
ステップ2もクリアです。
ステップ3:小さい素数で順番に割ってみる
最後のステップです。
残った素数である「7」から順番に割り算を試していきます。
「113」を7で割ってみると…
113 ÷ 7 = 16.14…
割り切れませんね。
次は、その次の素数「11」で割ってみます。
113 ÷ 11 = 10.27…
これも割り切れません。
実は、この割り算は「割る数 × 割る数」が、調べたい数(113)を超えたら終わりにしてOKです。
11 × 11 = 121で、113を超えました。
ここまで割り切れなかったので、「113」は素数であると判定できます。
まるでキャラクター?個性豊かな「名前付き素数」の世界
素数の中には、その特別な性質からユニークな名前が付けられているものたちがいます。
ここでは、まるで個性的なキャラクターのような「名前付き素数」の世界をのぞいてみましょう。
メルセンヌ素数:最大の素数記録を更新し続ける王者
「現在知られている、最も大きな素数は?」
この問いの答えは、ほぼ間違いなく「メルセンヌ素数」になります。
メルセンヌ素数とは、「2をn回掛けた数から1を引いた数」(2n – 1)の形で表される素数のことです。
- n=3 のとき: 23 – 1 = 8 – 1 = 7 (素数)
- n=5 のとき: 25 – 1 = 32 – 1 = 31 (素数)
- n=7 のとき: 27 – 1 = 128 – 1 = 127 (素数)
この形の数は、新しい巨大な素数を見つけるための探査プロジェクト「GIMPS」の対象となっており、現在見つかっている素数の中で最大のものは、このメルセンヌ素数の一種です。
まさに素数界の記録を更新し続ける「王者」のような存在ですね。
双子素数:いまだ未解決の「仲良しペア」の謎
隣り合う奇数がどちらも素数であるペアを「双子素数」と呼びます。
名前の通り、まるで仲良しの双子のような素数のペアです。
- (3, 5)
- (5, 7)
- (11, 13)
- (17, 19)
素数そのものは無限に存在することが証明されています。
しかし、この双子素数が無限に存在するのかどうかは、いまだに誰も証明できていない数学の大きな未解決問題の一つ「双子素数予想」として知られています。
回文素数・エマープ:言葉遊びのようなユニークな素数
数字の並び自体が面白いパターンを持つ素数も存在します。
回文素数は、前から読んでも後ろから読んでも同じになる素数のことです。「131」や「757」などがこれにあたります。まるで言葉遊びのようですね。
また、エマープ(emirp)という変わった名前の素数もあります。
これは素数(prime)を逆から書いた言葉で、その名の通り数字を逆から並べても、また別の素数になる数のことを指します。
- 13 → 逆から読むと 31 (どちらも素数)
- 17 → 逆から読むと 71 (どちらも素数)
- 37 → 逆から読むと 73 (どちらも素数)
このように、素数の世界には数学的な重要性だけでなく、パズルのような面白さも隠されています。
素数が現代社会を支えている?暗号技術との深い関係
「素数を勉強して、何の役に立つの?」
これは多くの人が一度は思う疑問ですが、その答えは「私たちのインターネット社会の安全を守っている」です。
あなたが普段、何気なく使っているネットショッピングやSNSの裏側では、素数が「暗号」として大活躍しています。
「素因数分解の難しさ」がインターネットの安全を守る鍵
なぜ素数が暗号になるのか。
その秘密は、前回解説した「算術の基本定理」の性質、特に「素因数分解」に隠されています。
素因数分解
コンピュータにとって、2つの巨大な素数を掛け合わせることは、いとも簡単な作業です。
例えば、電卓で「31 × 43」を計算するのは一瞬ですよね。
しかし、その逆の「掛け算の結果(例:1333)だけを見せられて、元の2つの素数(31と43)を当ててください」という問題になると、途端に難易度が跳ね上がります。
これが数百桁にもなる巨大な数になると、たとえ世界中のスーパーコンピュータを結集しても、元の素数のペアを見つけ出すには天文学的な時間がかかると言われています。
この「掛け算は簡単、でも素因数分解は極めて困難」という一方通行の性質が、現代のセキュリティを支える強力な鍵となっているのです。
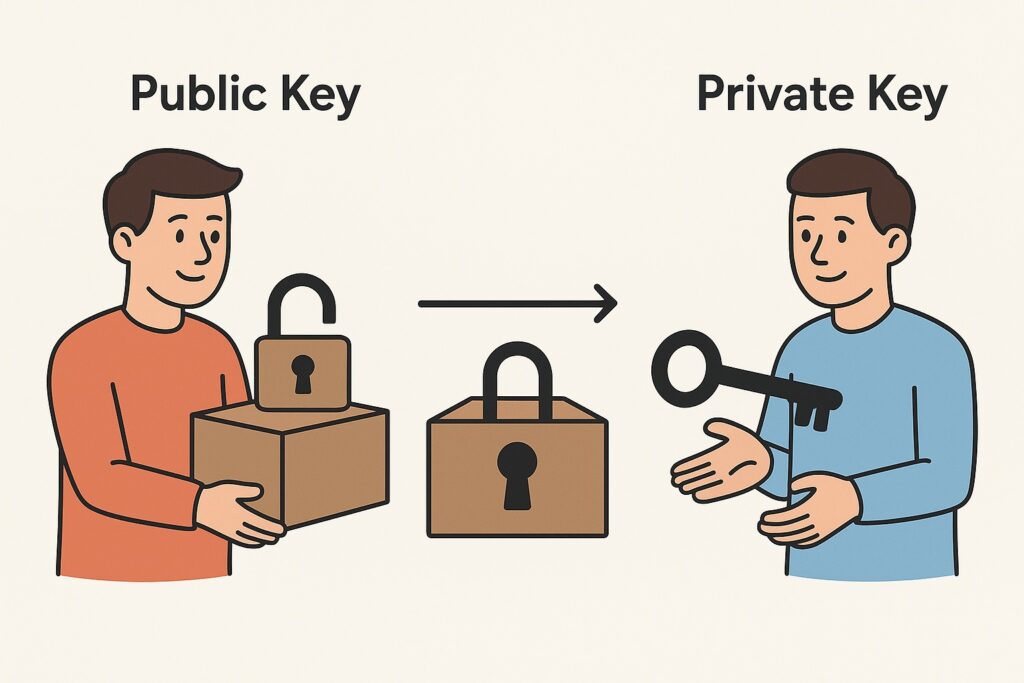
ネットショッピングを支える「RSA暗号」の仕組みとは
この素因数分解の難しさを利用した代表的な技術が「RSA暗号」です。
これは、現在のインターネット通信で最も広く使われている暗号方式の一つです。
仕組みを南京錠に例えてみましょう。
- 南京錠と鍵を用意する (鍵の生成)
受信者は、巨大な素数を使って、誰でも使える「公開鍵(開いた南京錠)」と、自分だけが持つ「秘密鍵(その南京錠を開ける唯一の鍵)」のペアを作ります。 - 南京錠を掛けて送る (暗号化)
送信者は、その「公開鍵(南京錠)」を使って、送りたいデータに鍵を掛けて(暗号化して)から送信します。 - 自分の鍵で開ける (復号)
データを受け取った受信者は、自分だけが持っている「秘密鍵」で、その南京錠を開けてデータを取り出します。
もし、通信の途中で悪意のある第三者がこのデータを盗み見ても、開けるための「秘密鍵」を持っていません。
そして、公開鍵(南京錠)から秘密鍵(合鍵)を作ろうとしても、巨大な素数の素因数分解という壁が立ちはだかるため、解読は事実上不可能なのです。
素数に関するよくある質問(FAQ)
ここでは、素数に関して多くの人が抱く素朴な疑問について、Q&A形式でお答えします。
Q1. 素数は無限にあるのですか?
A. はい、素数は無限に存在します。
これは、紀元前の古代ギリシャの数学者ユークリッドによって証明されています。
彼の証明は「もし素数が有限個しかないと仮定すると、必ず矛盾が生じてしまう。したがって、素数は無限に存在しなければならない」という、非常にエレガントな方法でした。
どれだけ大きな素数が見つかっても、その先に必ずまた別の素数が存在することが保証されています。
Q2. 完璧な「素数生成式」はありますか?
A. いいえ、残念ながらまだ見つかっていません。
代入すれば必ず素数が生まれるような、完璧な「素数生成式」は存在しないと考えられています。
歴史上、オイラーなどの天才数学者たちが「n2 + n + 41\)」のような、次々と素数を生み出す数式を発見しましたが、いずれもある特定の数で成り立たなくなってしまいました。
素数の出現パターンは、単純な数式で表せるほど簡単ではないのです。
Q3. 最も有名な未解決問題は何ですか?
A. 「リーマン予想」が最も有名で、数学における最重要問題の一つとされています。
これは、「素数がどのように分布しているか」という、素数の出現法則の根幹に関わる予想です。
もしリーマン予想が証明されれば、素数の謎の多くが解明されると考えられており、その影響は数学界にとどまりません。
この予想の証明には、100万ドル(1億円以上)の懸賞金がかけられています。
まとめ
この記事では、素数の基本的な定義から、その不思議な種類、そして現代社会の暗号技術を支える重要な役割までを解説しました。
素数は、数の世界の基本的な原子であると同時に、いまだ多くの謎を秘めた、奥深い研究対象です。
次にあなたが数字を目にしたとき、その背後に広がる素数の壮大な世界を、少しだけ想像してみてください。きっと、いつもの景色が少しだけ違って見えるはずです。





コメント