「ベクトル」と聞くと、
「なんだか難しそう…」
「矢印がたくさん出てきてよくわからない」
と、苦手意識を持ってしまう高校生も多いんじゃないでしょうか?
でも、大丈夫!ベクトルは、その正体さえつかんでしまえば、数学の世界をぐっと広げてくれる強力なツールになるんです。
この記事では、「ベクトルって一体何?」という基本的なところから、計算のルール、そして図形問題への応用まで、ゼロから一歩ずつ丁寧に解説していきます。たくさんの図を使いながら、まるで隣で友達が教えてくれるような感覚で読み進められるように工夫しました。この記事を読み終わる頃には、ベクトルの面白さに気づき、「なるほど、そういうことか!」と自信を持って言えるようになっているはずです。さあ、一緒にベクトルの世界の扉を開けてみましょう!
ベクトルって何?まずは基本のキから理解しよう
数学の教科書を開いて「ベクトル」の文字を見ると、なんだか身構えてしまいますよね。でも、実はベクトルは私たちの身の回りにあふれている、とてもシンプルな考え方なんです。まずは「ベクトルって、結局なんなの?」という一番大事なところから、一緒に見ていきましょう。
矢印に隠された意味!ベクトルの定義は「向き」と「大きさ」
突然ですが、天気予報で「北東の風、風速3m」と聞いたとき、どんなことをイメージしますか?
おそらく、「風が吹いてくる向き(北東)」と「風の強さ(風速3m)」の2つを思い浮かべますよね。
実は、これがベクトルの正体です。
このように、「向き」と「大きさ」という2つの情報セットで表される量のことを「ベクトル」と呼びます。
数学では、このベクトルをよく矢印(\rightarrow)で表現します。矢印の「向き」がベクトルの向きを、矢印の「長さ」がベクトルの大きさを表している、と考えるとイメージしやすいですよ。
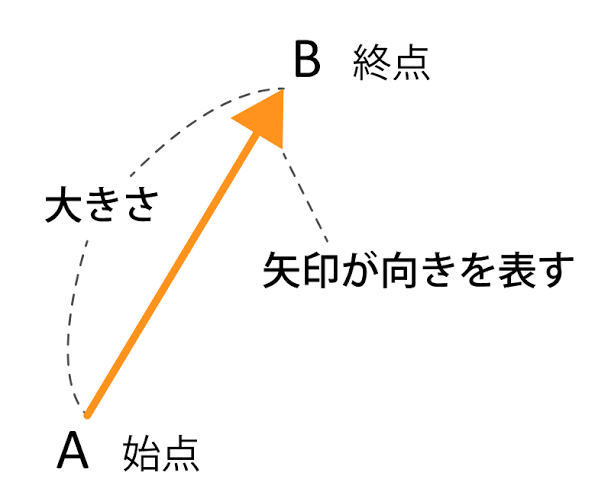
これだけは覚えよう!ベクトルの基本用語
ベクトルを学ぶ上で、いくつか基本的な言葉が出てきます。ここでしっかり押さえておきましょう。
- 有向線分(ゆうこうせんぶん):向きを持った線分のこと。ベクトルの具体的な形です。
- 始点(してん):矢印のはじまりの点のこと。
- 終点(しゅうてん):矢印の終わりの点のこと。
例えば、点Aから点Bに向かうベクトルは \vec{AB} と書き表します。この場合、Aが始点、Bが終点ですね。また、\vec{a} のように、1つの文字で表すこともよくあります。
ちなみに、ベクトルとよく比較される言葉に「スカラー」があります。これは向きを持たず、大きさだけで決まる量のこと。例えば、気温25℃、身長170cm、500円玉などがスカラーです。「向き」があるかないかが、ベクトルとの大きな違いです。
平行移動しても同じ?「等しいベクトル」の考え方
ベクトルには、とても大事なルールがあります。それは、「向きと大きさが同じなら、場所がどこにあっても同じベクトルとみなす」というルールです。
例えば、東京から東に100km進む矢印と、大阪から東に100km進む矢印を考えてみてください。
スタート地点は全く違いますが、「東に」という向きと「100km」という大きさが同じですよね。このとき、この2つのベクトルは「等しい」と言えるんです。
つまり、ベクトルは、その矢印を平行移動させてぴったり重ねることができれば、すべて同じものとして扱える、と覚えておきましょう。この「場所に縛られない」という性質が、後々とても重要になってきます。
ベクトルの足し算・引き算・実数倍【基本の計算】
ベクトルの正体がわかったところで、次はそのベクトルたちを計算する方法を学びましょう。「計算」といっても、普通の数字の計算とは少しイメージが違います。ここでも「矢印の図」を頭に思い浮かべるのが、理解への一番の近道ですよ。
ベクトルの足し算:矢印の「しりとり」で考えよう
ベクトルの足し算は、一言でいうと「2つの移動を合成する」ことです。
例えば、\vec{a} が「東に3歩進む」、\vec{b} が「北に4歩進む」というベクトルだとします。
このとき、\vec{a} + \vec{b} は、「東に3歩進んだ後、続けて北に4歩進む」という移動を表します。
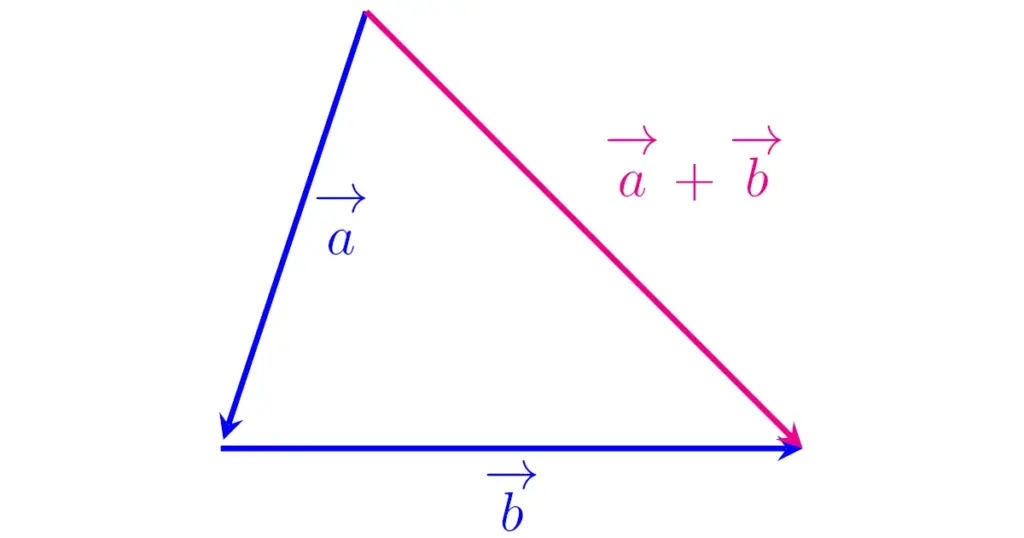
図で描くときは、1つめのベクトル(\vec{a})の終点(矢印の先)に、2つめのベクトル(\vec{b})の始点(矢印の根元)をつなげます。まるで矢印で「しりとり」をするイメージですね。
そして、最初の始点から最後の終点に向かって引いた1本の矢印、これが2つのベクトルを足した答え \vec{a} + \vec{b} になります。
ベクトルの引き算:「逆向きの矢印」を足してみよう
引き算は、少しだけ考え方を変えると簡単になります。それは、「引き算は、逆向きのベクトルの足し算である」と考える方法です。
ベクトル \vec{b} に対して、大きさが同じで向きだけが正反対のベクトルを -\vec{b} と書き、「逆ベクトル」と呼びます。
そして、\vec{a} - \vec{b} という計算は、\vec{a} + (-\vec{b}) とまったく同じ意味になります。
つまり、\vec{b} の矢印をくるっと180度ひっくり返して、それを \vec{a} に足し算すれば、それが引き算の答えになるのです。
もう一つの考え方として、2つのベクトルの始点をそろえて考える方法も便利です。始点をそろえたとき、「終点から終点へ向かうベクトル(引かれるベクトル\vec{a}の終点に向かう)」が引き算の答えになります。これは \vec{OA}-\vec{OB}=\vec{BA} という公式として、とてもよく使います。
ベクトルの実数倍:矢印を伸ばしたり縮めたり
ベクトルに普通の数字(スカラー)を掛ける計算を「実数倍」と言います。これはとても直感的で、ベクトルの向きを変えずに長さを変える操作です。
- 2\vec{a} :\vec{a} と向きは同じで、長さ(大きさ)が2倍のベクトル。
- \frac{1}{2}\vec{a} :\vec{a} と向きは同じで、長さ(大きさ)が半分のベクトル。
- -3\vec{a} :\vec{a} と向きが正反対で、長さ(大きさ)が3倍のベクトル。
このように、掛ける数字がプラスなら向きはそのまま、マイナスなら向きが正反対になります。そして、数字の大きさの分だけ、矢印が伸びたり縮んだりするわけですね。
【発展】0ベクトルと逆ベクトルとは?
最後に、計算で使う特別なベクトルを2つ紹介します。
0ベクトル(\vec{0})
これは、大きさが0のベクトルのことです。始点と終点が同じ「点」のようなベクトルをイメージしてください。数字の世界の「0」と同じで、どんなベクトルに足しても相手を変えない(\vec{a} + \vec{0} = \vec{a})という性質があります。
逆ベクトル
先ほど引き算で登場した、\vec{a} に対して大きさが同じで向きが正反対のベクトル -\vec{a} のことです。この2つを足すと、行って戻ってくることになるので、結果は \vec{0} になります。(\vec{a} + (-\vec{a}) = \vec{0})
ベクトルを数字で表す!「成分表示」をマスターしよう
これまで、ベクトルを矢印の図で考えてきました。でも、複雑な問題になるたびに図を描くのは少し大変ですよね。そこで登場するのが、ベクトルを「数字のペア」で表す「成分表示」という、とても便利な方法です。これが使えるようになると、ベクトルの計算が一気にスピードアップしますよ!
なぜ「成分」が必要なの?座標で考えるメリット
一番のメリットは、「ベクトルの問題を、ただの計算問題に変えられる」ことです。
これまでは「矢印をつなげて…」と考えていましたが、成分表示を使うと、ベクトルを座標平面の上の「座標」として扱えるようになります。そうすると、足し算や引き算が、単純な数字の計算だけでできるようになるんです。図形的なセンスに頼らなくても、機械的に、そして正確に答えが出せる。それが成分表示の最大の強みです。
ベクトルの成分表示とそのルール
ベクトルの成分表示は、とてもシンプルです。ベクトルの始点を座標平面の原点O(0, 0)に置いたとき、終点の座標がそのままそのベクトルの成分になります。
例えば、始点が原点Oで、終点がP(3, 4)となるベクトル \vec{p} があったとします。このとき、ベクトル \vec{p} の成分表示は \vec{p}=(3, 4) となります。3がx成分、4がy成分です。
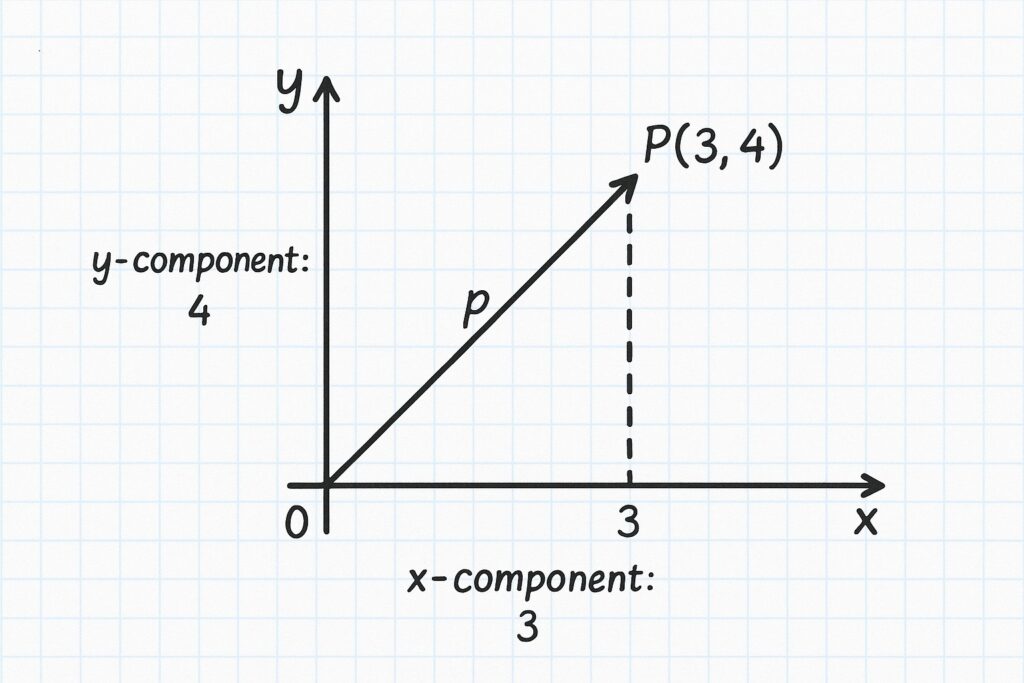
始点が原点でない場合、例えばA(x_1, y_1) からB(x_2, y_2)へ向かうベクトル\vec{AB}の成分は、「(終点の座標)-(始点の座標)」で計算できます。
つまり、\vec{AB}=(x_2-x_1, y_2-y_1) となります。これも非常に重要なルールなので、しっかり覚えておきましょう。
成分計算は超カンタン!足し算・引き算・実数倍
成分表示のすごいところは、あの面倒だった矢印の計算が、驚くほど簡単になる点です。
\vec{a}=(a_1, a_2)、\vec{b}=(b_1, b_2) とすると、計算は次のようになります。
- 足し算:\vec{a}+\vec{b} = (a_1+b_1, a_2+b_2)
(x成分同士、y成分同士をそれぞれ足すだけ!) - 引き算:\vec{a}-\vec{b} = (a_1-b_1, a_2-b_2)
(x成分同士、y成分同士をそれぞれ引くだけ!) - 実数倍:k\vec{a} = (ka_1, ka_2)
(x成分、y成分の両方に数を掛けるだけ!)
どうでしょうか?矢印のしりとりを考えるより、ずっと簡単で、計算ミスも減りそうですよね。
成分からベクトルの大きさを求める方法(三平方の定理)
成分はベクトルの「向き」と「大きさ」を表現したものですが、矢印の長さ、つまりベクトルの「大きさ」そのものを知りたいときもあります。
ベクトルの大きさは、絶対値の記号を使って |\vec{a}| のように表します。
\vec{a}=(a_1, a_2) の大きさは、原点(0, 0)と点(a_1, a_2)の間の距離を求めるのと同じです。これは、中学校で習った「三平方の定理」を使えば簡単に計算できます。
公式は次のようになります。
|\vec{a}| = \sqrt{a_1^2 + a_2^2}
x成分とy成分をそれぞれ2乗して足し合わせ、最後に平方根(ルート)をとれば、ベクトルの大きさが求められます。
2つのベクトルの関係を探る「内積」とは?
さあ、いよいよ高校数学ベクトルの最大の山場、「内積(ないせき)」です。多くの人が「?」となってしまう場所ですが、大丈夫。「何のためにこれを使うのか」という目的さえ分かってしまえば、決して怖いものではありません。一緒に乗り越えていきましょう!
内積の目的は「ベクトルの世界の掛け算」
内積は、一言でいうと「2つのベクトルが、どれくらい同じ方向を向いているか」を調べるための計算です。ベクトルの世界での「掛け算」のようなもの、と考えてみてください。
ただし、普通の掛け算とは少し違います。内積の計算結果は、ベクトルではなく、ただの数字(スカラー)になります。この数字がプラスで大きいほど「2つのベクトルは似た方向を向いている」、0に近ければ「お互い直角に近い関係だ」、マイナスなら「逆の方向を向いている」ということがわかる、便利な道具なんです。
内積の計算方法は2通り!定義式を覚えよう
内積には、計算方法が2つあります。どちらも非常に重要で、問題によって使い分ける必要があります。
| 計算方法 | この式を使う場面 | 公式 |
|---|---|---|
| 大きさとなす角で計算 | 図形的にベクトルの大きさと角度がわかっている時 | \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta |
| 成分で計算 | ベクトルの成分がわかっている時(最もよく使う) | \vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 |
内積で何がわかる?2つのベクトルの「なす角」を求めよう
「なぜ計算方法が2つもあるの?」と思ったかもしれません。実は、この2つの式を組み合わせることで、内積の最大のメリットである「2つのベクトルのなす角\thetaを求める」ことができるのです。
先ほどの2つの式は、どちらも同じ「内積」を表しているので、イコールで結ぶことができます。
|\vec{a}||\vec{b}|\cos\theta = a_1b_1 + a_2b_2
この式を \cos\theta について解くと、次の公式が導けます。
\cos\theta = \frac{a_1b_1 + a_2b_2}{|\vec{a}||\vec{b}|}
ベクトルの成分さえわかっていれば、この式で \cos\theta の値を計算でき、そこから角度 \theta がわかる、というわけです。
【超重要】内積が0なら、ベクトルは「垂直」!
内積の性質の中で、テストや入試で最もよく使われる、一番大事な性質がこれです。
もし2つのベクトルが垂直に交わっている場合、なす角は \theta=90^\circ ですよね。このとき、\cos90^\circ=0 なので、内積の定義式 \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta の右側がすべて0になります。
このことから、次の非常に重要な関係が成り立ちます。(\vec{a}\neq\vec{0}, \vec{b}\neq\vec{0}のとき)
\vec{a} \perp \vec{b} \Leftrightarrow \vec{a} \cdot \vec{b} = 0
つまり、「2つのベクトルが垂直であること」と「内積が0であること」は、全く同じ意味なのです。成分で言えば a_1b_1 + a_2b_2 = 0 となり、垂直かどうかを簡単にチェックできる、超強力なツールです。
【図形への応用】ベクトルで図形問題を解いてみよう
これまで学んできたベクトルの知識は、実は図形問題を解くときに絶大なパワーを発揮します。「場所に縛られない」のがベクトルの特徴でしたが、ここでは逆にベクトルを使って「点の位置」を正確に表現し、図形の性質を解き明かしていく方法を見ていきましょう。
全てのベクトルの基準点!「位置ベクトル」という考え方
図形問題を考えるとき、点の「位置」は非常に重要です。そこで、どこか1点を「基準点O」として固定し、その基準点Oから見た各点の位置をベクトルで表すという考え方が「位置ベクトル」です。
例えば、点Aの位置ベクトルは、基準点Oから点Aへ向かうベクトル \vec{OA} のことで、これを \vec{a} のように小文字1文字でシンプルに表すのが一般的です。
この考え方の最大のメリットは、2点間のベクトルを位置ベクトルで表現できる点にあります。例えば、ベクトル\vec{AB}は、引き算のルールを使うと、
\vec{AB} = \vec{OB} - \vec{OA} = \vec{b} - \vec{a}
のように、「(終点の位置ベクトル)-(始点の位置ベクトル)」という形で表せます。すべてのベクトルを基準点Oからのベクトルに変換できるため、計算の見通しが非常に良くなるのです。
内分点・外分点の公式もベクトルなら怖くない
数学IIで学んだ「内分点・外分点の公式」を覚えていますか?少し複雑な式でしたが、あれも位置ベクトルを使うと、なぜ成り立つのかがスッキリ理解できます。
線分ABを m:n に内分する点Pの位置ベクトルを \vec{p} とすると、\vec{p}は次の式で表せます。
\vec{p} = \frac{n\vec{a} + m\vec{b}}{m+n}これは、点Aの位置ベクトル \vec{a} と点Bの位置ベクトル \vec{b} を、n:m の比率で混ぜ合わせた点にPがある、とイメージすると分かりやすいです。分母が比の合計、分子は比をクロスして掛け算する(nを\vec{a}に、mを\vec{b}に)と覚えると便利です。ちなみに外分点の場合は、n を -n に置き換えるだけで同じ公式が使えます。
直線の方程式をベクトルで表す方法
ベクトルを使うと、直線そのものを式で表すこともできます。これを「ベクトル方程式」と呼びます。
「点A(位置ベクトル \vec{a})を通り、ベクトル \vec{d} に平行な直線」を考えてみましょう。
この直線の上にある任意の点P(位置ベクトル \vec{p})は、次のようにしてたどり着けます。
- まず、基準点Oから点Aまで移動する(\vec{a})
- 次に、点Aからベクトル \vec{d} の方向に好きなだけ進む(t\vec{d})
この動きを1つの式にまとめると、次のようになります。
\vec{p} = \vec{a} + t\vec{d} (t は任意の実数)
この式が、直線のベクトル方程式です。\vec{d} を方向ベクトル、実数 t を媒介変数と呼びます。t の値がいろいろな実数に変わることで、点Pが直線上を動いていく、というイメージですね。この考え方は、3次元の空間図形を考える上でも基本となる、とても重要なものです。
それでもわからない?ベクトルのよくある質問(FAQ)
最後に、ベクトルを学んでいると多くの人が疑問に思う点をQ&A形式でまとめました。ここを読めば、さらに理解が深まるはずです。
Q1. ベクトルとスカラーの違いは何ですか?
A. 一番の違いは「向き」の情報があるかないかです。
- ベクトル:「向き」と「大きさ」の2つの情報を持つ量です。(例:東向きに時速50kmで進む自動車の「速度」)
- スカラー:「大きさ」だけを持つ量です。(例:自動車のメーターが示す「速さ」時速50km)
このように、向きを考える必要があるかどうかが、両者を見分けるポイントになります。
Q2. ベクトルを学ぶと、どんないいことがありますか?
A. 主に3つのメリットがあります。
- 物理現象を理解できる:力の合成・分解や速度など、物理の世界はベクトルであふれています。ベクトルは物理を学ぶ上での必須言語です。
- 図形問題の視野が広がる:座標を使わなくても、図形の位置関係や性質を証明できるようになり、問題へのアプローチ方法が増えます。
- CGやゲームに応用されている:実は、3Dゲームでキャラクターを動かしたり、CGで物体を滑らかに動かしたりする最先端技術の裏側では、ベクトルの計算がフル活用されています。
ベクトルを学ぶことは、より高度な科学や技術の世界につながる第一歩だと言えます。
Q3. 内積の計算結果がマイナスになるのはなぜですか?
A. それは、2つのベクトルのなす角が鈍角(90°より大きい)だからです。
内積の定義式 \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta を思い出してください。
この式で、大きさである |\vec{a}| と |\vec{b}| は必ず0以上なので、内積のプラス・マイナスの符号は \cos\theta の符号だけで決まります。
- 角度 \theta が鋭角(<90°)なら \cos\theta はプラス → 内積はプラス
- 角度 \theta が鈍角(>90°)なら \cos\theta はマイナス → 内積はマイナス
つまり、内積がマイナスということは、2つのベクトルが互いに反対方向を向いている、という関係性を示しているのです。
まとめ:ベクトルの世界へようこそ!
お疲れ様でした!この記事では、ベクトルとは何かという基本から、計算、応用までを一つずつ見てきました。もう一度、大切なポイントを振り返ってみましょう。
- ベクトルの正体は「向き」と「大きさ」を持つ矢印。
- 計算は「成分」を使うと、ただの数字の計算になりとても楽になる。
- 「内積」を使えば、2つのベクトルのなす角や垂直関係がわかる。
- 「位置ベクトル」は、図形問題を解くための強力な武器になる。
この記事を最後まで読んだあなたは、もうベクトルの基礎をしっかりと理解できています。知識を本物の力に変えるには、実際に問題を解いてみることが一番です。ぜひ教科書や問題集の問題に挑戦して、「わかった!」という喜びをさらに深めていってくださいね。応援しています!
にほんブログ村(算数・数学科教育)




