今回の記事はこちらの問題、アジア太平洋の第1問です。
三角形ABCがある。点Hは三角形ABCの垂心であり、点M,Nは各々辺AB,ACの中点である。Hは四角形BMNCの内部にあり、三角形BMH,CNHの外接円は互いに接している。Hを通りBCに平行な直線が、三角形BMH,CNHの外接円とそれぞれH以外の点K,Lで交わるとする。直線MKとNLの交点をF、三角形MHNの内心をJとするとき、FJ=FAを示せ。ただし、XYで線分XYの長さを表すものとする。
とても図を作りにくい設定になっています。
正確な図を作ろうとしたらこの問題を解くための計算だけでは済みません。
問題の状況を図にするとこうなるようです。
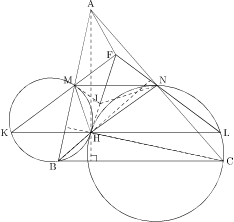
色々値を書き込んでいくと、どうやらFが何らかの円の中心になってくれればいけそうな気がします。
色々な角度の関係を探ったら以下のような結果が出ました。
Hは三角形ABCの垂心であり三角形ABCの内部にあるので
∠ ABH=180°- ∠ BAC – 90° = 90° – ∠ BAC
∠ ACH=180°- ∠ CAB – 90° = 90° – ∠ BAC
すなわち∠ ABH=∠ ACHがわかる。
∠ ABH=180°- ∠ BAC – 90° = 90° – ∠ BAC
∠ ACH=180°- ∠ CAB – 90° = 90° – ∠ BAC
すなわち∠ ABH=∠ ACHがわかる。
またHが四角形BMNCの内部にあることから円周角の定理により
∠ MKH=∠ MBH = ∠ ABH
∠ NLH=∠ NCH = ∠ ACH
すなわち∠ MKH=∠ NLHがわかる。
さらに中点連結定理よりMNはBCに平行なのでKLとも平行であることがわかり、同位角の関係から
∠ FMN=∠ FKH = ∠ MKH
∠ FNM=∠ FLH = ∠ NLH
すなわち∠ FMN=∠ FNMがわかり、したがって三角形FMNはFM=FNの二等辺三角形であることがわかる。
ということで、中心Fで半径がFMである円が使えそうです。実際これを思いつくと解けます。
他の方針だとどうなるかはわかりません。
そこで中心をFとし、M,Nを通る円を考える。
∠ MFN=180°-∠ FMN- ∠ FNM = 180°-(90°-∠ BAC)- (90°-∠ BAC) = 2∠ BAC
なので弧MNの中心角は2∠ BACに等しいので円周角は∠ BACとなり、
またFとAはMNからみて同じ側にくるのですなわちこの円はAを通ることがわかる。
∠ MFN=180°-∠ FMN- ∠ FNM = 180°-(90°-∠ BAC)- (90°-∠ BAC) = 2∠ BAC
なので弧MNの中心角は2∠ BACに等しいので円周角は∠ BACとなり、
またFとAはMNからみて同じ側にくるのですなわちこの円はAを通ることがわかる。
ということで、FA=FM=FNがわかりました。あとはこの円がJを通ることがいえれば成功です。
三角形BMHの外接円とCNHの外接円は点Hを共有するので接点として考えられる点はHに限られる。
そこでこの接点から共通の接線を辺BCと反対方向にのばし、線分HM,HNのそれぞれとなす角α,βを考えると
α=∠ MBH = 90°-∠BAC,β=∠ NCH = 90°-∠BAC
と等しくなるのですなわちこの半直線は∠MHNを二等分することから半直線HJに一致することがわかる。
よって∠MHN = 180°-2∠BACであることから
∠ HMN+ ∠HNM= 2∠BACとなるので
∠MJN=180°-(∠ HMN+ ∠HNM)/2 = 180°- ∠BACとなり、
すなわち∠MAN+∠MJN=180°がわかる。
よって四角形AMJNは3点A,M,Nを通る円に内接し、その円の中心はFであることからFA=FJがいえる。□
そこでこの接点から共通の接線を辺BCと反対方向にのばし、線分HM,HNのそれぞれとなす角α,βを考えると
α=∠ MBH = 90°-∠BAC,β=∠ NCH = 90°-∠BAC
と等しくなるのですなわちこの半直線は∠MHNを二等分することから半直線HJに一致することがわかる。
よって∠MHN = 180°-2∠BACであることから
∠ HMN+ ∠HNM= 2∠BACとなるので
∠MJN=180°-(∠ HMN+ ∠HNM)/2 = 180°- ∠BACとなり、
すなわち∠MAN+∠MJN=180°がわかる。
よって四角形AMJNは3点A,M,Nを通る円に内接し、その円の中心はFであることからFA=FJがいえる。□
どうにか図も作ることができました。条件をみたす座標系を出そうとしたら6次方程式になってしまった…