テレビでは今年も最強の頭脳 日本一決定戦! 頭脳王が2/3に放送されました。
今回も1次選抜はホームページで気軽に解けることから、11万人以上の挑戦者が受けたようです。
ちなみに、2019年度の1次選抜も実施されており、私も突破しました。(応募はしていない)
さて、頭脳王といえど数学や算数の問題はみなさんでも電卓を使えば正解できるはずです!
ここでは放送された中から算数数学の思考で解ける7問を取り上げます(権利が必要そうなものはこの中にないはず)。
今回はちょっと高度な確率の問題。
この平面に長さ4cmの針を無作為に落とす。
このとき針が平行線と重なる確率を求めよ。
これを解くには確率密度という概念が必要です。
・ある連続的な値をとる確率変数tについて、f(t)をtのとりうる値全体で積分した時の値が1になるような関数fを確率密度関数とよぶ。
また、この仮定を利用します。
・平行線の角度を固定して針と平行線とのなす角がsとなる確率密度関数f(s)と、針の中心とそこから下方向で最も近い平行線との距離がdとなる確率密度関数g(d)を考えたとき、f(s)は-π<s≦πの範囲、g(d)は0≦d<12cmの範囲で定数になるとする。
ここから下に解説が表示されます。
まずは針の回転角を固定して考えましょう。
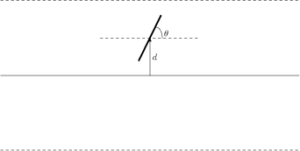
針の先端と平行線がなす角をθ(上下前後を決めて-π~π)とすると、
針の中心と平行線との距離が-2|sin θ|~2 |sin θ| (cm)の範囲(マイナスなら下)にくるときに平行線と交わります。
1本の平行線で考える範囲は上方向12(cm)ということでしたので(外れたら別の平行線を使う)、
回転角を固定したときに平行線と重なる確率は|4 sint|/12=|sint|/3 となります。
この値をtで積分するわけですが、今回は-π~πまでで同じ確率、ということですのでそれぞれのtについてこのような確率分布になる関数はf(t)=1/(2π)ということになります。
したがって確率はf(t)|sint|/3 = |sin t|/(6π)を積分して求めることになります。これは偶関数ですので計算すると
2[-cost/(6π)]0π=2/3π
と求められます。
問題自体は「ビュッフォンの針」として知られていますが確率密度関数を持ち出すので慣れない計算になると思います。
最後はジグソーパズルを紹介します。